Chapter 2: Geographic data in R

Key Learnings from, and Solutions to the exercises in Chapter 2 of the book Geocomputation with R by Robin Lovelace, Jakub Nowosad and Jannes Muenchow.

Geocomputation with R
Textbook Solutions
Author

Aditya Dahiya

Published

November 3, 2024

2.1 Introduction

  • Geographic Data Models: Vector and raster models are foundational.
    • Vector Model: Represents geographic data as points, lines, and polygons with precise boundaries; commonly used in social sciences for features like human settlements.
    • Raster Model: Divides surfaces into cells; useful in environmental sciences, often based on remote sensing and aerial data. Scalable and consistent over large areas.
  • Choosing a Model:
    • Vector is often used in social sciences.
    • Raster is prevalent in environmental studies.
  • R Implementation:
    • Use sf for vector data.
    • Use terra for raster data.
library(sf)           # Simple Features in R
library(terra)        # Raster Data in R
library(spData)       # Spatial Datasets
library(spDataLarge)  # Large Spatial Datasets
library(tidyverse)    # Data Wrangling and Visualization

2.2 Vector Data

  • Vector Data: Represents geographic features using points, lines, and polygons based on coordinate reference systems (CRS).
    • Example: London’s coordinates c(-0.1, 51.5) in geographic CRS or c(530000, 180000) in projected CRS (British National Grid).
  • CRS Overview:
    • Geographic CRS uses lon/lat (0° longitude and latitude origin).
    • Projected CRS, like the British National Grid, is based on Easting/Northing coordinates with positive values.
  • Key dependencies / libraries used by the sf Package:
    • GDAL: Handles geographic data formats
    • PROJ: For CRS transformations
    • GEOS: Supports planar geometry for projected data
    • S2: Manages spherical geometry for unprojected data (e.g., lon/lat), toggleable with sf::sf_use_s2(FALSE).
  • Geometry Engines:
    • Planar (GEOS): For 2D projected data.
    • Spherical (S2): For 3D unprojected data.

2.2.1 Introduction to Simple Features

  • Simple Features (SF): Hierarchical model by OGC (Open Geospatial Consortium); supports multiple geometry types.
  • Core Types: sf package in R supports 7 core geometry types (points, lines, polygons, and their “multi” versions).
  • Library Integration: sf replaces sp, rgdal, rgeos; unified interface for GEOS (geometry), GDAL (data I/O), PROJ (CRS).
  • Non-Planar Support: Integrates s2 for geographic (lon/lat) operations, used by default for accuracy on spherical geometries.
  • Data Storage: SF objects are data frames with a spatial column (geometry or geom).
  • Vignettes: Documentation accessible with vignette(package = "sf") for practical use and examples.
  • Plotting: plot(sf_object) maps all variables, unlike single-map GIS tools.
  • Summary: summary() gives spatial and attribute data insights.
  • Subset: SF objects subsettable like data frames, retaining spatial metadata.
world
Simple feature collection with 177 features and 10 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: -180 ymin: -89.9 xmax: 180 ymax: 83.64513
Geodetic CRS:  WGS 84
# A tibble: 177 × 11
   iso_a2 name_long continent region_un subregion type  area_km2     pop lifeExp
 * <chr>  <chr>     <chr>     <chr>     <chr>     <chr>    <dbl>   <dbl>   <dbl>
 1 FJ     Fiji      Oceania   Oceania   Melanesia Sove…   1.93e4  8.86e5    70.0
 2 TZ     Tanzania  Africa    Africa    Eastern … Sove…   9.33e5  5.22e7    64.2
 3 EH     Western … Africa    Africa    Northern… Inde…   9.63e4 NA         NA  
 4 CA     Canada    North Am… Americas  Northern… Sove…   1.00e7  3.55e7    82.0
 5 US     United S… North Am… Americas  Northern… Coun…   9.51e6  3.19e8    78.8
 6 KZ     Kazakhst… Asia      Asia      Central … Sove…   2.73e6  1.73e7    71.6
 7 UZ     Uzbekist… Asia      Asia      Central … Sove…   4.61e5  3.08e7    71.0
 8 PG     Papua Ne… Oceania   Oceania   Melanesia Sove…   4.65e5  7.76e6    65.2
 9 ID     Indonesia Asia      Asia      South-Ea… Sove…   1.82e6  2.55e8    68.9
10 AR     Argentina South Am… Americas  South Am… Sove…   2.78e6  4.30e7    76.3
# ℹ 167 more rows
# ℹ 2 more variables: gdpPercap <dbl>, geom <MULTIPOLYGON [°]>
names(world)
 [1] "iso_a2"    "name_long" "continent" "region_un" "subregion" "type"     
 [7] "area_km2"  "pop"       "lifeExp"   "gdpPercap" "geom"     
class(world)
[1] "sf"         "tbl_df"     "tbl"        "data.frame"
########### THE GEOMETRY COLUMN IS STICKY ################
summary(world["lifeExp"])
    lifeExp                 geom    
 Min.   :50.62   MULTIPOLYGON :177  
 1st Qu.:64.96   epsg:4326    :  0  
 Median :72.87   +proj=long...:  0  
 Mean   :70.85                      
 3rd Qu.:76.78                      
 Max.   :83.59                      
 NA's   :10
Code 
plot(world)
Figure 1: The basic plot() function on a sf object produced multiple plots, one for each of the non-geometry variables (columns) in the plotted dataset.

2.2.2 Why Simple Features?

  • Cross-Compatibility: SF model is compatible with many GIS tools (e.g., QGIS, PostGIS), enabling easy data transfer.
  • Advantages of sf in R:
    • Data Handling: Fast reading/writing of spatial data.
    • Plotting: Improved plotting speed and performance.
    • Data Frame-Like: sf objects behave like data frames.
    • Consistent Naming: sf functions are intuitive, starting with st_.
    • Tidyverse-Friendly: Works well with |> and integrates with tidyverse packages.
  • Data Import Options:
    • read_sf(): Imports data as a tidy tibble (quietly).
    • st_read(): Imports data as a base R data frame (verbose).
  • Popularity: sf is the primary package for spatial vector data in R, preferred over alternatives like spatstat and terra.
world_dfr <- st_read(system.file("shapes/world.shp", package = "spData"))
## Reading layer `world' from data source 
##   `C:\Users\dradi\AppData\Local\R\win-library\4.3\spData\shapes\world.shp' 
##   using driver `ESRI Shapefile'
## Simple feature collection with 177 features and 10 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -180 ymin: -89.9 xmax: 180 ymax: 83.64513
## Geodetic CRS:  WGS 84
world_dfr <- read_sf(system.file("shapes/world.shp", package = "spData"))

class(world_dfr)
## [1] "sf"         "tbl_df"     "tbl"        "data.frame"

2.2.3 Basic Maps

  • Plotting in sf:
    • plot() creates multi-panel plots for multiple variables or a single-panel plot for one variable.
    • Supports fixed color customization using col and border arguments.
Code 
plot(world)
Figure 2: The base plot() function creates a faceted output with a map for each variable other than geometry
  • Layering Plots: Add layers to existing plots with add = TRUE. Use reset = FALSE for plots with a key.
  • Overlaying Data: Circles representing population size can be plotted using cex and st_centroid().
  • Bounding Box Expansion: expandBB adjusts the plot boundaries (bottom, left, top, right).
  • Limitations: Base plot() is simple but limited in functionality; use tmap for advanced maps.

2.2.4 Geometry Types

  • Geometry Basics:
    • Core components of simple features; sf supports 18 types.
    • Focus on 7 common types: POINT, LINESTRING, POLYGON, MULTIPOINT, MULTILINESTRING, MULTIPOLYGON, GEOMETRYCOLLECTION.
  • Encoding Standards:
    • WKB (Well-known binary): Hexadecimal, computer-friendly format.
    • WKT (Well-known text): Human-readable format, often shown for explanation.
  • Common Geometries:
    • POINT: Single coordinate (e.g., POINT (5 2)).
    • LINESTRING: Connected sequence of points (e.g., LINESTRING (1 5, 4 4, 4 1, 2 2, 3 2)).
    • POLYGON: Closed ring of points (e.g., POLYGON ((1 5, 2 2, 4 1, 4 4, 1 5))).
  • Multi-Geometries:
    • MULTIPOINT: Multiple points (e.g., MULTIPOINT (5 2, 1 3, 3 4, 3 2)).
    • MULTILINESTRING: Multiple linestrings (e.g., MULTILINESTRING ((1 5, 4 4, 4 1, 2 2, 3 2), (1 2, 2 4))).
    • MULTIPOLYGON: Multiple polygons (e.g., MULTIPOLYGON (((1 5, 2 2, 4 1, 4 4, 1 5), (0 2, 1 2, 1 3, 0 3, 0 2)))).
  • Geometry Collection:
    • Mix of geometry types (e.g., GEOMETRYCOLLECTION (MULTIPOINT (5 2, 1 3, 3 4, 3 2), LINESTRING (1 5, 4 4, 4 1, 2 2, 3 2))).

2.2.5 The sf Class

  • Structure of sf Objects: Composed of geometries (sfc object) and non-geographic attributes (data.frame or tibble).

  • Creation of sf Objects: Steps:

    1. Create geometry (sfg) with functions like st_point()

    2. Convert to geometry column (sfc) with CRS using function st_sfc(..., crs = "...")

    3. Combine attributes (data.frame) with sfc using function st_sf(..., geometry = ...)

  • Characteristics:

    • sf objects have dual class: sf and data.frame.
    • Spatial attributes stored in a geometry column.
    • sf behaves like a data.frame but with spatial extension.

2.2.6 Simple Feature Geometries (sfg)

An sfg object represents a single simple feature geometry. A simple feature geometry column (sfc) is a collection of sfg objects and can also include information about the coordinate reference system (CRS) being used.

Geometries can be created using st_ functions or imported from existing spatial files.

  • sfg Creation Functions:
    • st_point(): Create a single point.
    • st_linestring(): Create a linestring.
    • st_polygon(): Create a polygon.
    • st_multipoint(): Create a multipoint.
    • st_multilinestring(): Create a multilinestring.
    • st_multipolygon(): Create a multipolygon.
    • st_geometrycollection(): Create a geometry collection.
  • Input Data Types:
    • Numeric Vector: Single points.
    • Matrix: Sets of points for multipoint or linestring.
    • List: Complex structures for multilinestrings, (multi)polygons, or geometry collections.
  • Examples:
Code 

# Create a point
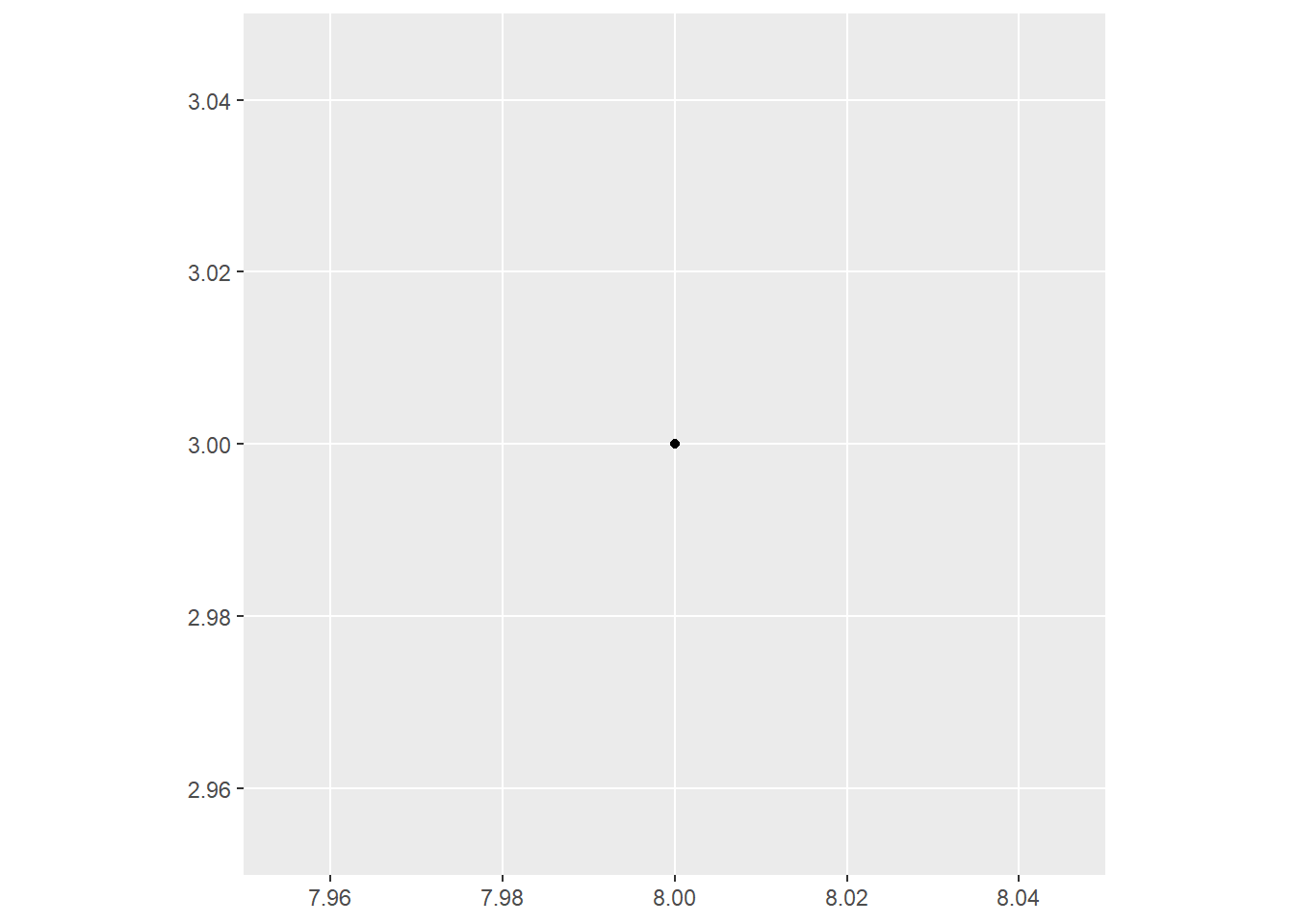
point <- st_point(c(8, 3))  # POINT (8 3)
print(point)
ggplot(point) +
  geom_sf()

# Create a multipoint
multipoint_matrix <- rbind(c(8, 3), c(2, 5), c(5, 7), c(7, 3))
multipoint <- st_multipoint(multipoint_matrix)  # MULTIPOINT ((8 3), (2 5), (5 7), (7 3))
print(multipoint)
ggplot(multipoint) +
  geom_sf()

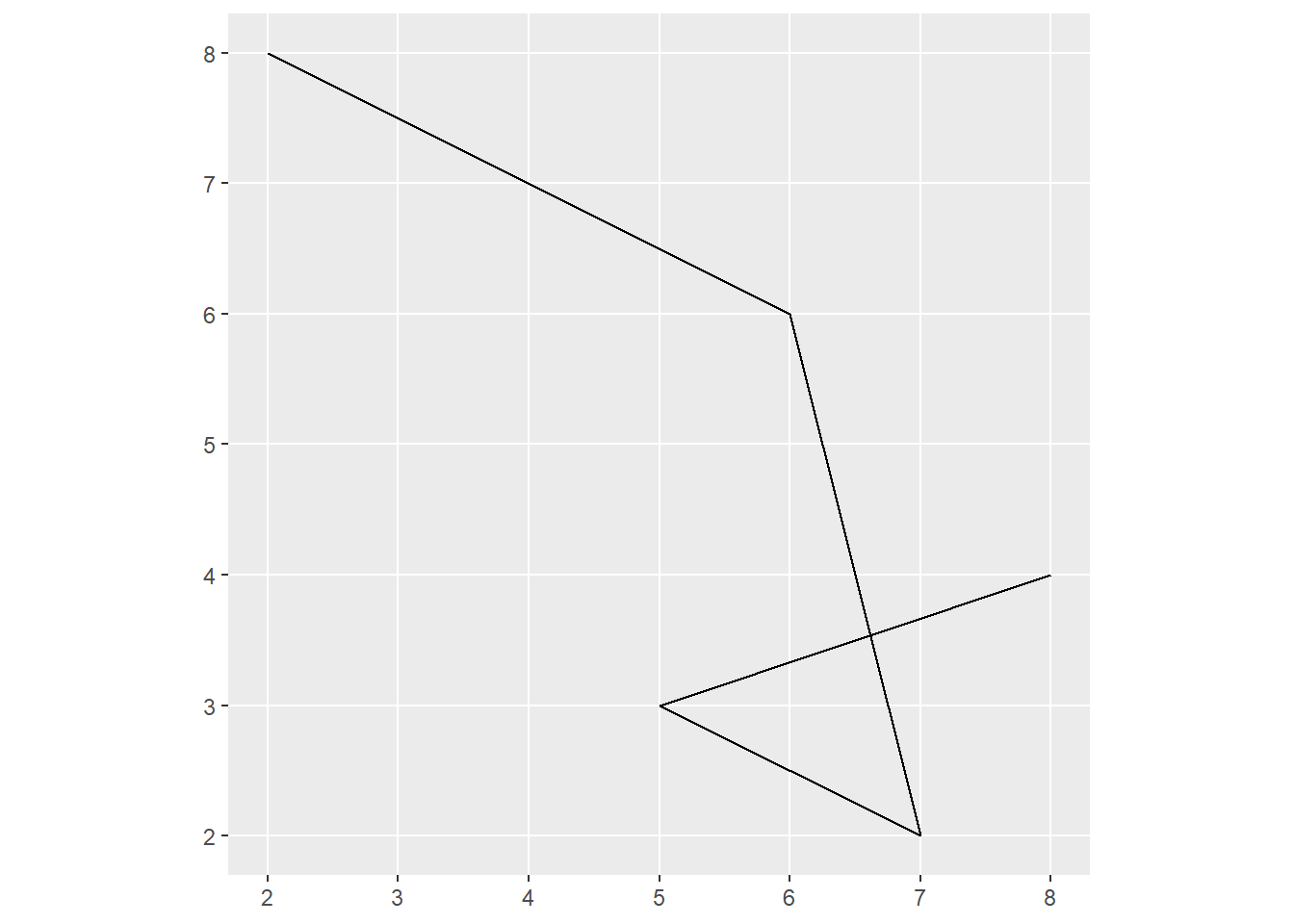
# Create a linestring
linestring_matrix <- rbind(c(2, 8), c(6, 6), c(7, 2), c(5, 3), c(8, 4))
linestring <- st_linestring(linestring_matrix)  # LINESTRING (2 8, 6 6, 7 2, 5 3, 8 4)
print(linestring)
ggplot(linestring) +
  geom_sf()

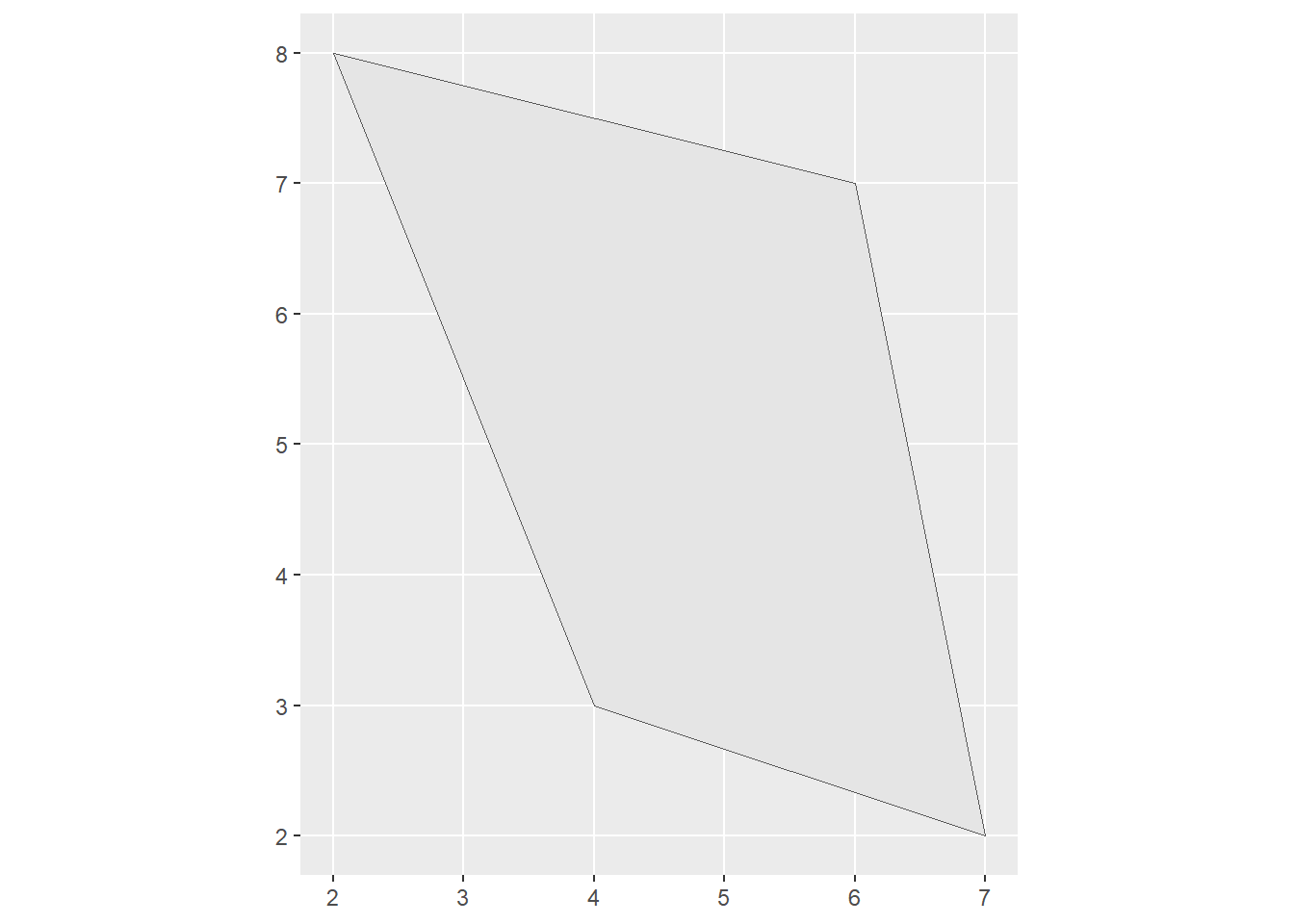
# Create a polygon
polygon_list <- list(rbind(c(2, 8), c(4, 3), c(7, 2), c(6, 7), c(2, 8)))
polygon <- st_polygon(polygon_list)  # POLYGON ((2 8, 4 3, 7 2, 6 7, 2 8))
print(polygon)
ggplot(polygon) +
  geom_sf()

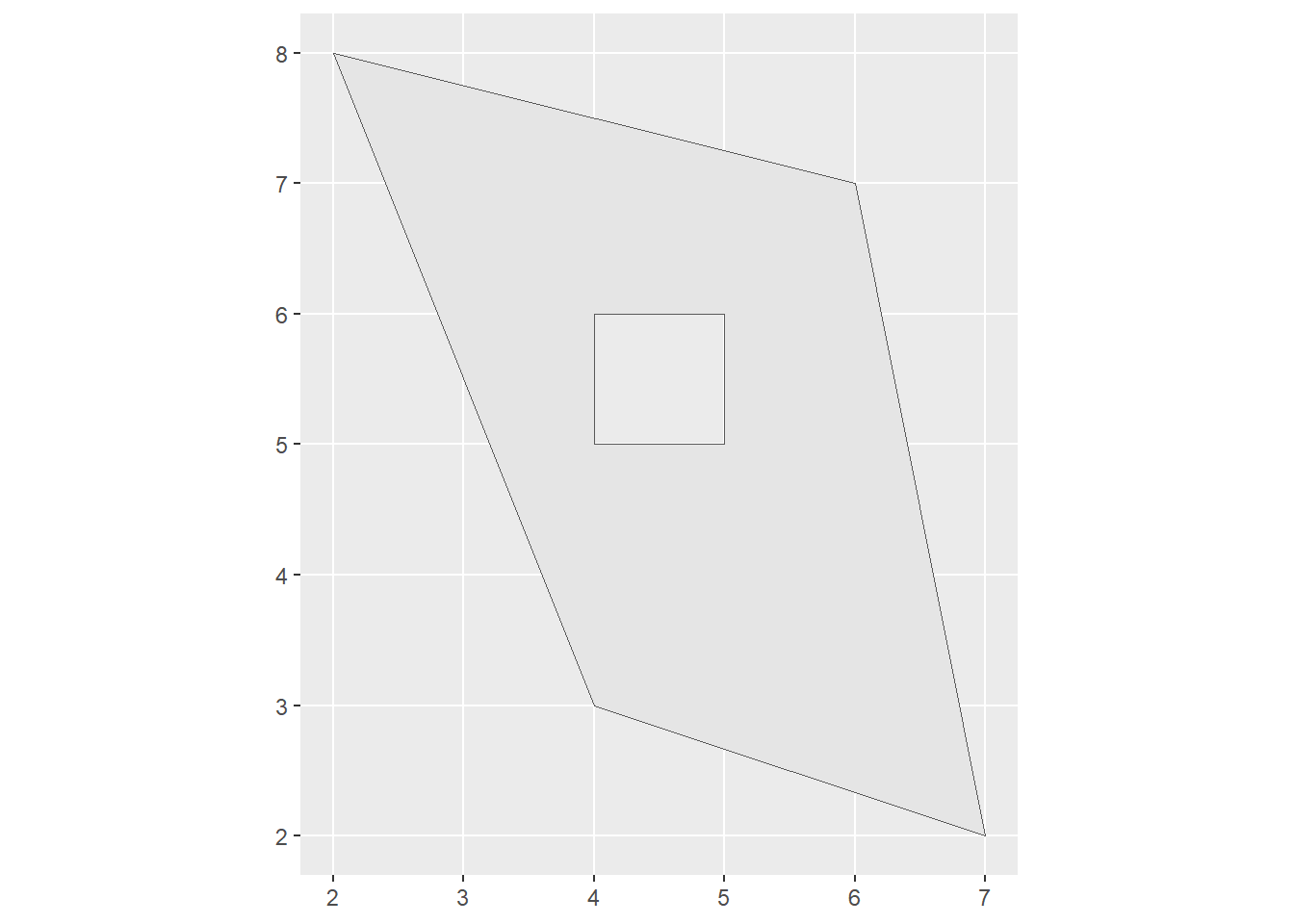
# Polygon with a hole
polygon_border <- rbind(c(2, 8), c(4, 3), c(7, 2), c(6, 7), c(2, 8))
polygon_hole <- rbind(c(4, 6), c(5, 6), c(5, 5), c(4, 5), c(4, 6))
polygon_with_hole_list <- list(polygon_border, polygon_hole)
polygon_with_hole <- st_polygon(polygon_with_hole_list)  # POLYGON with a hole
print(polygon_with_hole)
ggplot(polygon_with_hole) +
  geom_sf()

# Create a multilinestring
multilinestring_list = list(
  rbind(c(2, 8), c(6, 6), c(7, 2), c(5, 3), c(8, 4)),
  rbind(c(3, 2), c(5, 8))
)
multilinestring = st_multilinestring(multilinestring_list)  # MULTILINESTRING
print(multilinestring)
ggplot(multilinestring) +
  geom_sf()

# Create a multipolygon
multipolygon_list = list(
  list(rbind(c(2, 8), c(4, 3), c(7, 2), c(6, 7), c(2, 8))),
  list(rbind(c(0, 3), c(2, 3), c(2, 4), c(0, 4), c(0, 3)))
)
multipolygon = st_multipolygon(multipolygon_list)  # MULTIPOLYGON
print(multipolygon)
ggplot(multipolygon) +
  geom_sf()

# Create a geometry collection
geometrycollection_list = list(st_multipoint(multipoint_matrix), st_linestring(linestring_matrix))
geometry_collection = st_geometrycollection(geometrycollection_list)  # GEOMETRYCOLLECTION
print(geometry_collection)
ggplot(geometry_collection) +
  geom_sf()
(a) A point
(b) A multipoint
(c) A linestring
(d) A polygon
(e) Polygon with a hole
(f) Multilinestring
(g) Multipolygon
(h) Geometry Collection
Figure 3: Creating different sample geometry objects in R with {sf}

2.2.8 The sfheaders Package

  • Overview:
    • sfheaders (Cooley 2024) is an R package designed to efficiently create and manipulate sf objects from vectors, matrices, and data frames.
    • It does not rely on the sf library and instead uses underlying C++ code, enabling faster operations and the potential for further development with compiled code.
  • Compatibility:
    • Although separate from sf, it is fully compatible, producing valid sf objects like sfg, sfc, and sf.
  • Key Functionality:
    • Converts:
      • Vector → sfg_POINT
      • Matrix → sfg_LINESTRING
      • Data Frame → sfg_POLYGON
    • Creates sfc and sf objects using similar syntax.
  • Advantages:
    • sfheaders is optimized for high-speed ‘deconstruction’ and ‘reconstruction’ of sf objects and casting between geometry types, offering faster performance than sf in many cases.

2.2.9 Spherical Geometry Operations with S2

  • Concept:
    • Spherical geometry operations acknowledge Earth’s roundness, as opposed to planar operations that assume flat surfaces.
    • Since sf version 1.0.0, R integrates with Google’s S2 spherical geometry engine, enabling accurate global spatial operations.
    • S2 supports operations like distance, buffer, and area calculations, allowing accurate geocomputation on a spherical Earth model.
    • Known as a Discrete Global Grid System (DGGS), S2 is similar to other systems like H3, which is a global hexagonal index.
  • S2 Mode:

    • By default, S2 is enabled in sf. Verify with:

      sf_use_s2()

    • Turning Off S2:

      sf_use_s2(FALSE)
  • S2 Limitations and Edge Cases:
    • Some operations may fail due to S2’s stricter definitions, potentially affecting legacy code. Error messages such as Error in s2_geography_from_wkb ... might require turning off S2.
  • Recommendation:
    • Keep S2 enabled for accurate global calculations unless specific operations necessitate its deactivation.

2.3 Raster Data

  • The raster data model represents the world as a continuous grid of cells (pixels). Focuses on regular grids, where each cell is of constant size, though other grid types (e.g., rotated, sheared) exist.
  • Structure:
    • Comprises a raster header and a matrix of equally spaced cells.
    • The raster header includes:
      • CRS (Coordinate Reference System)
      • Extent (geographical area covered)
      • Origin (starting point, often the lower left corner; the terra package defaults to the upper left).
    • Extent is defined by:
      • Number of columns (ncol)
      • Number of rows (nrow)
      • Cell size resolution
  • Cell Access and Modification:
    • Cells can be accessed and modified by:
      • Cell ID
      • Explicitly specifying row and column indices.
    • This matrix representation is efficient as it avoids storing corner coordinates (unlike vector polygons).
  • Data Characteristics:
    • Each cell can hold a single value, which can be either:
      • Continuous (e.g., elevation, temperature)
      • Categorical (e.g., land cover classes).
  • Applications:
    • Raster maps are useful for continuous phenomena (e.g., temperature, population density) and can also represent discrete features (e.g., soil classes).

2.3.1 R Packages for Working with Raster Data

  • Several R packages for reading and processing raster datasets have emerged over the last two decades. The raster package was the first significant advancement in R’s raster capabilities when launched in 2010. It was the premier package until the development of terra and stars, both offering powerful functions for raster data.
  • This book emphasizes terra, which replaces the older, slower raster package.
  • Comparison of terra and stars:
Feature terra stars
Primary Focus Regular grids Supports regular, rotated, sheared, rectilinear, and curvilinear grids
Data Structure One or multi-layered rasters Raster data cubes with multiple layers, time steps, and attributes
Memory Management Uses C++ code and pointers for data storage Uses lists of arrays for smaller rasters; file paths for larger ones
Vector Data Integration Uses its own class SpatVector but supports sf objects Closely related to vector objects/functions in sf
Functions & Methods Large number of built-in, purpose-specific functions (e.g., re-sampling, cropping) Mix of built-in functions (st_ prefix), existing dplyr functions, and custom methods for R functions
Conversion Between Packages Conversion to stars with st_as_stars() Conversion to terra with rast()
Performance Generally optimized for speed and memory efficiency Flexible, but performance varies based on data type and structure
Best Use Cases Single or multi-layer rasters; fast processing Complex data cubes with layers over time and multiple attributes
Programming Language Basis Primarily C++ R with some C++ integration

2.3.2 Introduction to terra

  • The terra package is designed for handling raster objects in R, supporting a range of functions to create, read, export, manipulate, and process raster datasets.
    • While its functionality is similar to the older raster package, terra offers improved computational efficiency.
    • Despite terra’s advantages, the raster class system remains popular due to its widespread use in other R packages.
    • terra provides seamless translation between the two object types using functions like raster(), stack(), and brick() for backward compatibility.
  • Key Features:
    • Low-Level Functionality: Includes functions that help in building new tools for raster data processing.
    • Memory Management: Supports processing of large raster datasets by dividing them into smaller chunks for iterative processing, allowing operations beyond available RAM capacity.
Code 
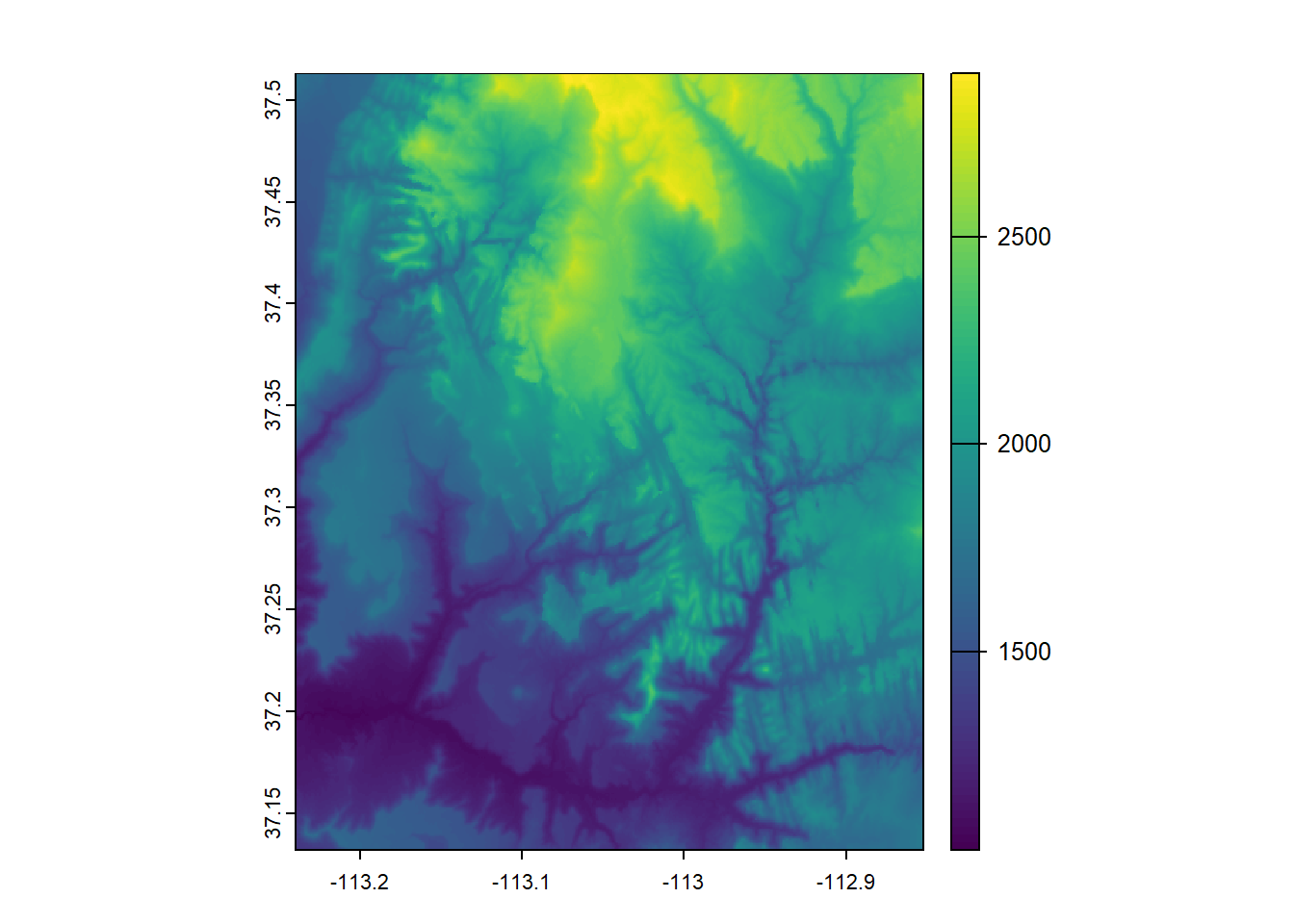
raster_filepath <- system.file("raster/srtm.tif", 
                              package = "spDataLarge")
my_rast <- rast(raster_filepath)

class(my_rast)
## [1] "SpatRaster"
## attr(,"package")
## [1] "terra"

ext(my_rast)
## SpatExtent : -113.239583212784, -112.85208321281, 37.1320834298579, 37.5129167631658 (xmin, xmax, ymin, ymax)

print(my_rast)
## class       : SpatRaster 
## dimensions  : 457, 465, 1  (nrow, ncol, nlyr)
## resolution  : 0.0008333333, 0.0008333333  (x, y)
## extent      : -113.2396, -112.8521, 37.13208, 37.51292  (xmin, xmax, ymin, ymax)
## coord. ref. : lon/lat WGS 84 (EPSG:4326) 
## source      : srtm.tif 
## name        : srtm 
## min value   : 1024 
## max value   : 2892
  • Dedicated Reporting Functions:
    • dim(): Number of rows, columns, and layers.
    • ncell(): Total number of cells (pixels).
    • res(): Spatial resolution.
    • ext(): Spatial extent.
    • crs(): Coordinate reference system (CRS).
    • inMemory(): Checks if data is stored in memory or on disk.
    • sources: Shows file location.
  • Accessing Full Function List:
    • Run help("terra-package") to see all available terra functions.

2.3.3 Basic Map-Making

  • Plotting with terra:
    • The terra package offers a simple way to create basic visualizations using the plot() function, specifically designed for SpatRaster objects.
Code 
plot(my_rast)
Figure 4: An example raster data displayed with {terra} using plot()
  • Advanced Plotting Options:
    • plotRGB(): A specialized function in terra for creating color composite plots using three layers (e.g., red, green, blue bands) from a SpatRaster object.
    • tmap Package (Tennekes 2018): Useful for creating both static and interactive maps for raster and vector data.
    • rasterVis Package (2023): Includes functions such as levelplot() to create advanced visualizations, including faceted plots for displaying changes over time.

2.3.4 Raster Classes

  • The SpatRaster class in terra represents raster objects. Rasters are commonly created by reading a file using rast()
    • terra supports reading various formats via GDAL, only loading the header and a file pointer into RAM.
  • Creating Rasters from Scratch: Use rast() to make new raster objects:
    • Fills values row-wise from the top left corner.
    • Resolution depends on rows, columns, and extent; defaults to degrees (WGS84 CRS).
Code 
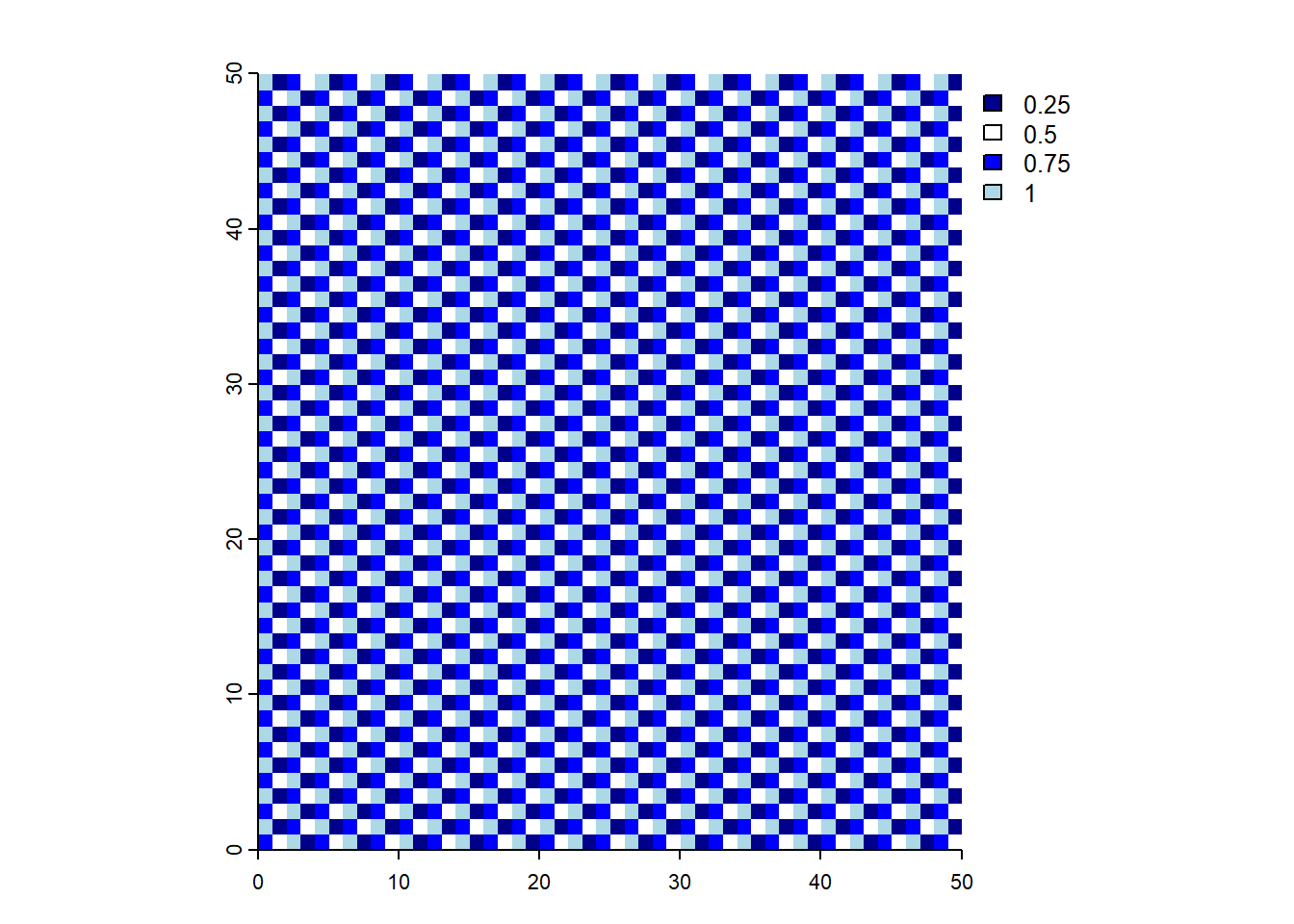
# Create a new SpatRaster object: a checkerboard design
new_raster = rast(nrows = 50, ncols = 50, 
                  xmin = 0, xmax = 50, 
                  ymin = 0, ymax = 50,
                  vals = rep(c(1, 0.25, 0.75, 0.5), 
                             times = 12)) 


# Plot the new raster
plot(new_raster, 
     col = c("darkblue", 
             "white",
             "blue",
             "lightblue"), # Use blue and white for the design
     axes = TRUE, 
     box = FALSE)
Figure 5: Creating a new raster from scratch
  • Handling Multi-Layer Rasters:

    • SpatRaster supports multi-layer rasters, such as satellite or time-series data:

      • Use nlyr() to get the number of layers:

      • Access layers with [[ or $.

      • Use subset() for layer extraction:

  • Combining Raster Layers:
    • Merge SpatRaster layers using c():
  • Saving SpatRaster Objects:
    • Since they often point to files, direct saving to .rds or .rda isn’t feasible.
    • Solutions:
      1. wrap(): Creates a temporary object for saving or cluster use.
      2. writeRaster(): Saves as a regular raster file.

2.4 Coordinate Reference Systems

  • CRSs (Coordinate Reference Systems) are essential for spatial data, defining how spatial elements correspond to the Earth’s surface (or other celestial bodies).
  • Types of CRSs:
    • Geographic CRSs:
      • Represent data on a three-dimensional surface (e.g., latitude and longitude).
      • Coordinate units are typically degrees.
    • Projected CRSs:
      • Represent data on a two-dimensional, flat plane.
      • Transform spherical Earth data into a flat map.
      • Coordinate units can be in meters, feet, etc.

2.4.1 Geographic Coordinate Reference Systems

  • Geographic CRSs use longitude and latitude to identify locations on Earth.
    • Longitude: Measures East-West position relative to the Prime Meridian.
    • Latitude: Measures North-South position relative to the equatorial plane.
    • Distances are measured in angular units (degrees), not meters, impacting spatial measurements (explored further in Section 7).
  • The Earth can be modeled as spherical or ellipsoidal.
    • Spherical models: Simplify calculations by assuming Earth is a perfect sphere.
    • Ellipsoidal models: More accurately represent Earth with distinct equatorial and polar radii. The equatorial radius is about 11.5 km longer than the polar radius due to Earth’s compression.
  • Datum refers to the model describing the relationship between coordinate values and actual locations on Earth. A datum consists of:

    1. Ellipsoid: An idealized mathematical model of the Earth’s shape, which helps to approximate the Earth’s surface.

    2. Origin Point: A fixed starting point for the coordinate system, where the ellipsoid is anchored to Earth.

    3. Offset and Orientation: How the ellipsoid is aligned with respect to the actual shape of the Earth.

  • The two types of Datums are: —
    • Geocentric datum (e.g., WGS84): Centered at Earth’s center of gravity, providing global consistency but less local accuracy.
    • Local datum (e.g., NAD83): Adjusted for specific regions to better align with the Earth’s surface, accounting for local geographic variations (e.g., mountain ranges).

2.4.2 Projected Coordinate Reference Systems

  • Projected CRSs are based on geographic CRSs and use map projections to represent Earth’s three-dimensional surface in Easting and Northing (x and y) values. These CRSs rely on Cartesian coordinates on a flat surface, with an origin and linear units (e.g., meters).
  • Deformations:
    • The conversion from 3D to 2D inherently introduces distortions. Projected CRSs can only preserve one or two of the following properties:
      • Area: Preserved in equal-area projections.
      • Direction: Preserved in azimuthal projections.
      • Distance: Preserved in equidistant projections.
      • Shape: Preserved in conformal projections.

Types of Projections and Their Characteristics

Type of Projection Description Common Properties Preserved Best Used For
Conic Projects Earth’s surface onto a cone. Area, shape Maps of mid-latitude regions
Cylindrical Projects Earth’s surface onto a cylinder. Direction, shape World maps
Planar (Azimuthal) Projects onto a flat surface at a point or line. Distance, direction Polar region maps

Deformations by Projection Type

Property Definition Projection Type That Preserves It
Area The relative size of regions is maintained. Equal-area projections (e.g., Albers)
Direction Bearings from the center are accurate. Azimuthal projections (e.g., Lambert)
Distance Correct distances are preserved along specific lines or from specific points. Equidistant projections (e.g., Equirectangular)
Shape Local angles and shapes are maintained, though areas are distorted. Conformal projections (e.g., Mercator)
  • Use the Map Projection Explorer for details.
  • Use st_crs() for querying CRSs in sf objects and crs() for terra objects.
Code 
sf_proj_info(type = "proj") |> 
  as_tibble() |> 
  gt::gt() |> 
  gt::cols_label_with(fn = snakecase::to_title_case) |> 
  gtExtras::gt_theme_espn() |> 
  gt::opt_interactive()
Table 1: A list of the available projections supported by the PROJ library

2.5 Units

  • CRSs include spatial units information, which is crucial for accurately interpreting distance and area.

  • Cartographic best practices suggest adding scale indicators on maps to show the relationship between map and ground distances.

  • Units in sf Objects:

    • sf objects natively support units for geometric data, ensuring outputs from functions like st_area() come with a units attribute.
    • This feature, supported by the units package, avoids confusion across different CRSs, which may use meters, feet, etc.
    • To convert units, use units::set_units()

  • Units in Raster Data:

    • Unlike sf, raster packages do not natively support units.
    • Users should be cautious when working with raster data to convert units properly.
    • An example to calculate the area of India in square meters and then, square kilometres
# Load required libraries
library(sf)
library(units)

# Calculate the area of India in square meters
india_area <- rnaturalearth::ne_countries() |> 
  filter(admin == "India") |> 
  st_area()
india_area
3.150428e+12 [m^2]
# Convert area to square kilometers
print(paste("Area of India in square kilometers:", format(set_units(india_area, km^2))))
[1] "Area of India in square kilometers: 3150428 [km^2]"
# Convert area to hectares
print(paste("Area of India in hectares:", format(set_units(india_area, ha))))
[1] "Area of India in hectares: 315042827 [ha]"
# Convert area to acres
print(paste("Area of India in acres:", format(set_units(india_area, acre))))
[1] "Area of India in acres: 778484666 [acre]"

2.6 Exercises

E1

Using summary() on the geometry column of the world data object in the spData package provides valuable information about the spatial characteristics of the dataset:

  1. Geometry Type:
    • The output will indicate the type of geometries present in the world data object. Here, it is MULTIPOLYGON suggesting that the dataset represents the outlines of countries or regions in MULTIPLOYGON formats.
  2. Number of Countries:
    • The summary will show the number of geometries or features present, which corresponds to the number of countries or regions represented in the world dataset. Here, it is 177 countries.
  3. Coordinate Reference System (CRS):
    • The output will include details about the CRS, and in the present case it is EPSG:4326.
summary((spData::world$geom))
 MULTIPOLYGON     epsg:4326 +proj=long... 
          177             0             0

E2

To generate the world map, you can run the following code (as shown in Section 2.2.3):

Code 
library(spData)
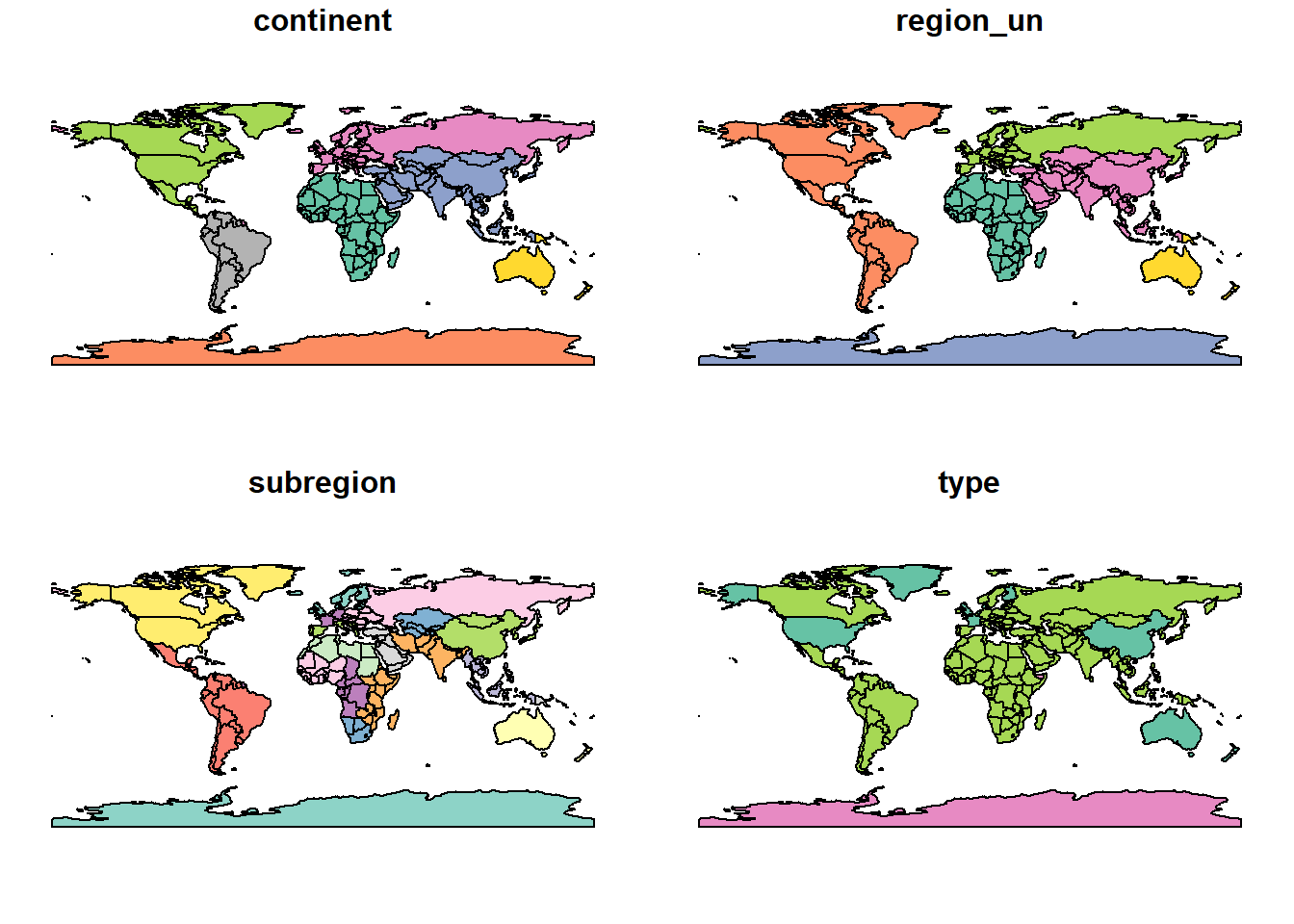
plot(world[3:6])
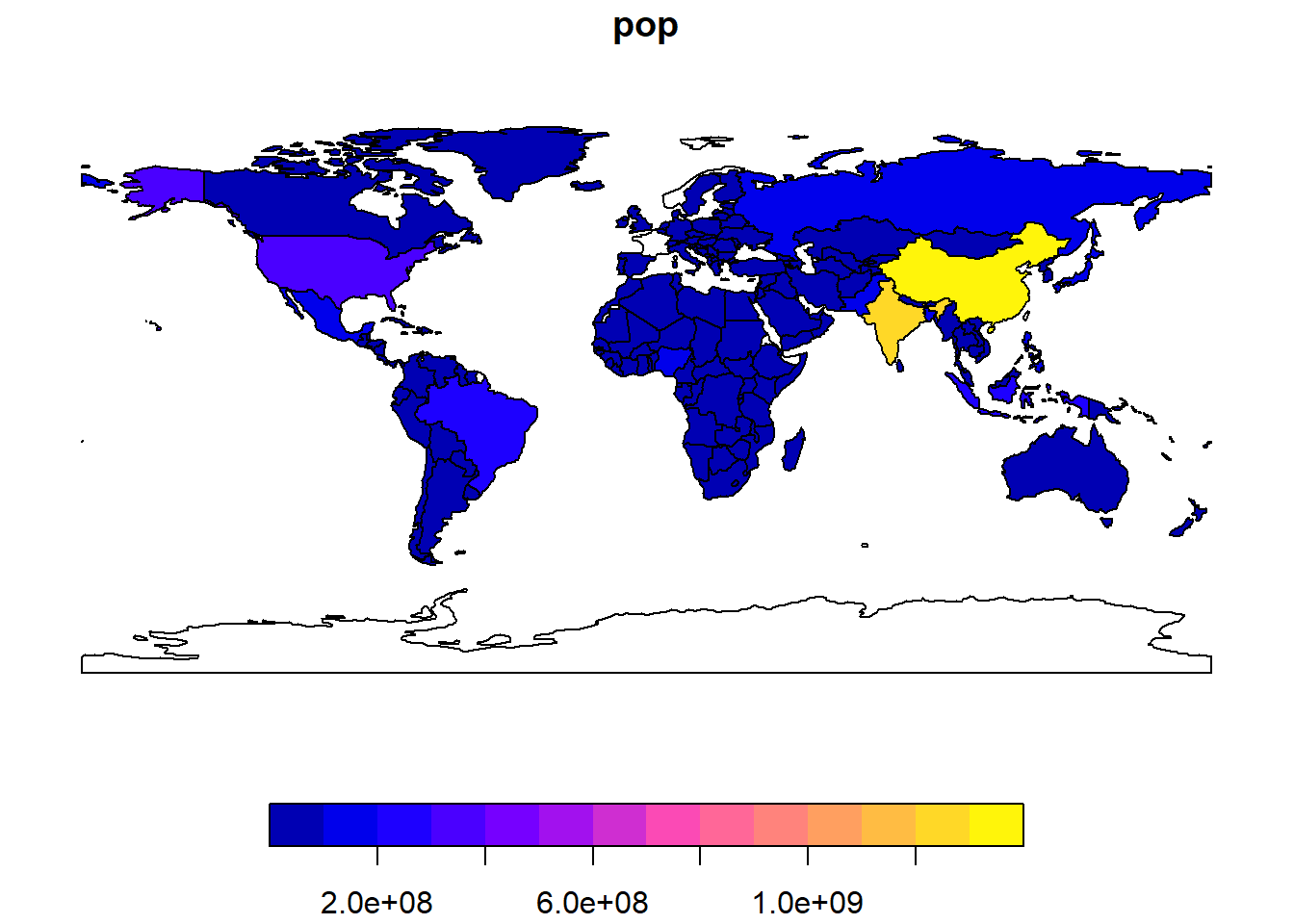
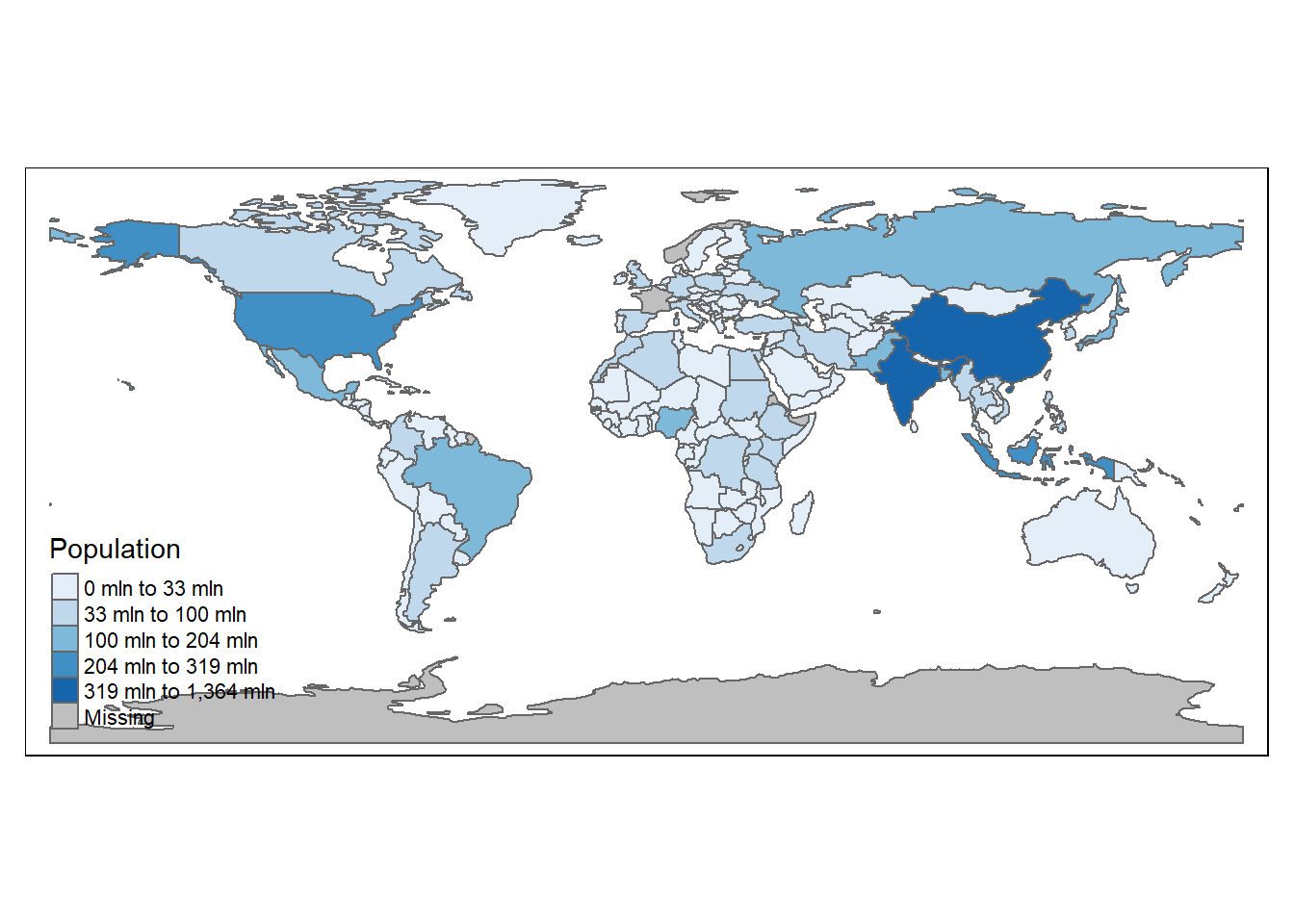
plot(world["pop"])
Figure 6: Reproducing Figure 2.4 of the book
Figure 7: Reproducing Figure 2.4 of the book
  • Similarities:
    1. The map displays country boundaries and highlights the global population distribution as shown in the book.
    2. The color scale representing population data is consistent with that described in the book, with larger populations shown with more intense colors.
  • Differences:
    1. The aspect ratio or positioning of the map might vary depending on your screen resolution and window size.
    2. The color theme and legend display may differ if your R setup or graphic device uses default settings different from those in the book.
  • cex Argument: This parameter controls the size of plotting symbols in R. It is a numeric value that acts as a multiplier for the default size of symbols.
    • Setting cex to values larger than 1 enlarges symbols, while values less than 1 shrink them.
  • Reason for cex = sqrt(world$pop) / 10000 : The code sets cex to sqrt(world$pop) / 10000 to scale the size of the points on the map in proportion to the population of each country. This square root transformation is used to moderate the variation in symbol sizes because population values can vary significantly between countries. Dividing by 10,000 helps to reduce the symbol size to a reasonable range for plotting.

Other Ideas: —

  • Bubble Plot: Overlay a bubble plot on the map with points sized by population.
Code 
plot(world["pop"])
points(st_coordinates(st_centroid(world$geom)), 
       cex = sqrt(world$pop) / 5000, 
       col = "red", pch = 19)

  • Choropleth Map: Use color gradients to represent population density.
Code 
library(tmap)
tm_shape(world) +
  tm_polygons("pop", style = "jenks", 
              palette = "Blues", 
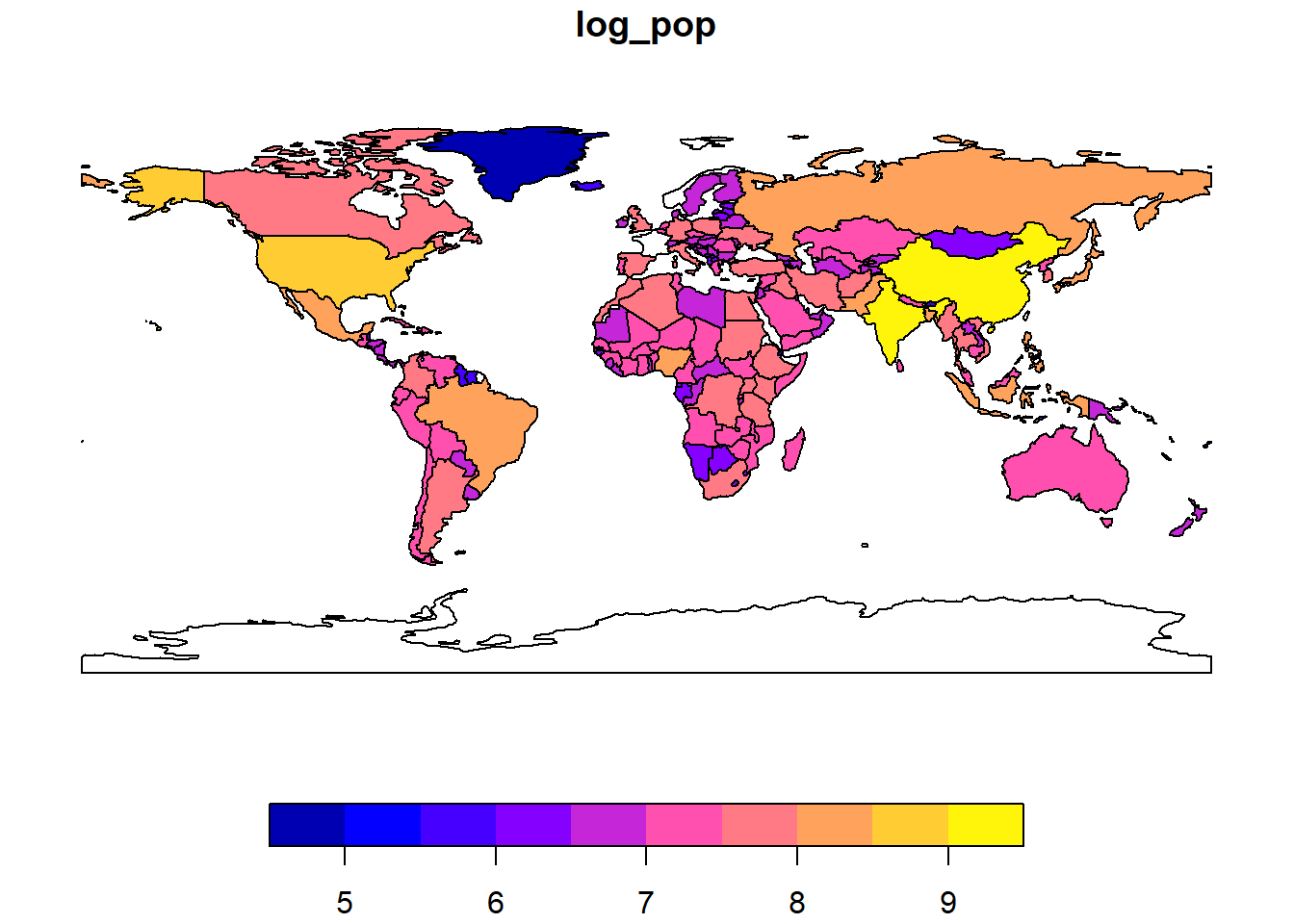
              title = "Population")

  • Log Transformation: Visualize population using a log scale for better differentiation.
Code 
world$log_pop = log10(world$pop + 1)
plot(world["log_pop"])

E3

To create a map of Nigeria in context and customize it using the plot() function, you can follow these steps:

Step 1: Load Necessary Libraries and Data: Make sure you have the spData package loaded and access to the world spatial data.

Step 2: Plotting Nigeria in Context: You can plot Nigeria by subsetting the world data and adjusting parameters such as lwd (line width), col (color), and expandBB (expanding the bounding box). Here’s an example code snippet:

Step 3: Annotating the Map: To annotate the map with text labels, you can use the text() function. Here’s an example where we add the name of Nigeria and its capital, Abuja:

Step 4: Exploring the text() Documentation

  • lwd: This argument controls the line width for the borders of the countries.
  • col: This argument sets the fill color for the countries. You can customize it based on your preference.
  • expandBB: This argument expands the bounding box of the plot, which can help visualize nearby areas more clearly.

E4

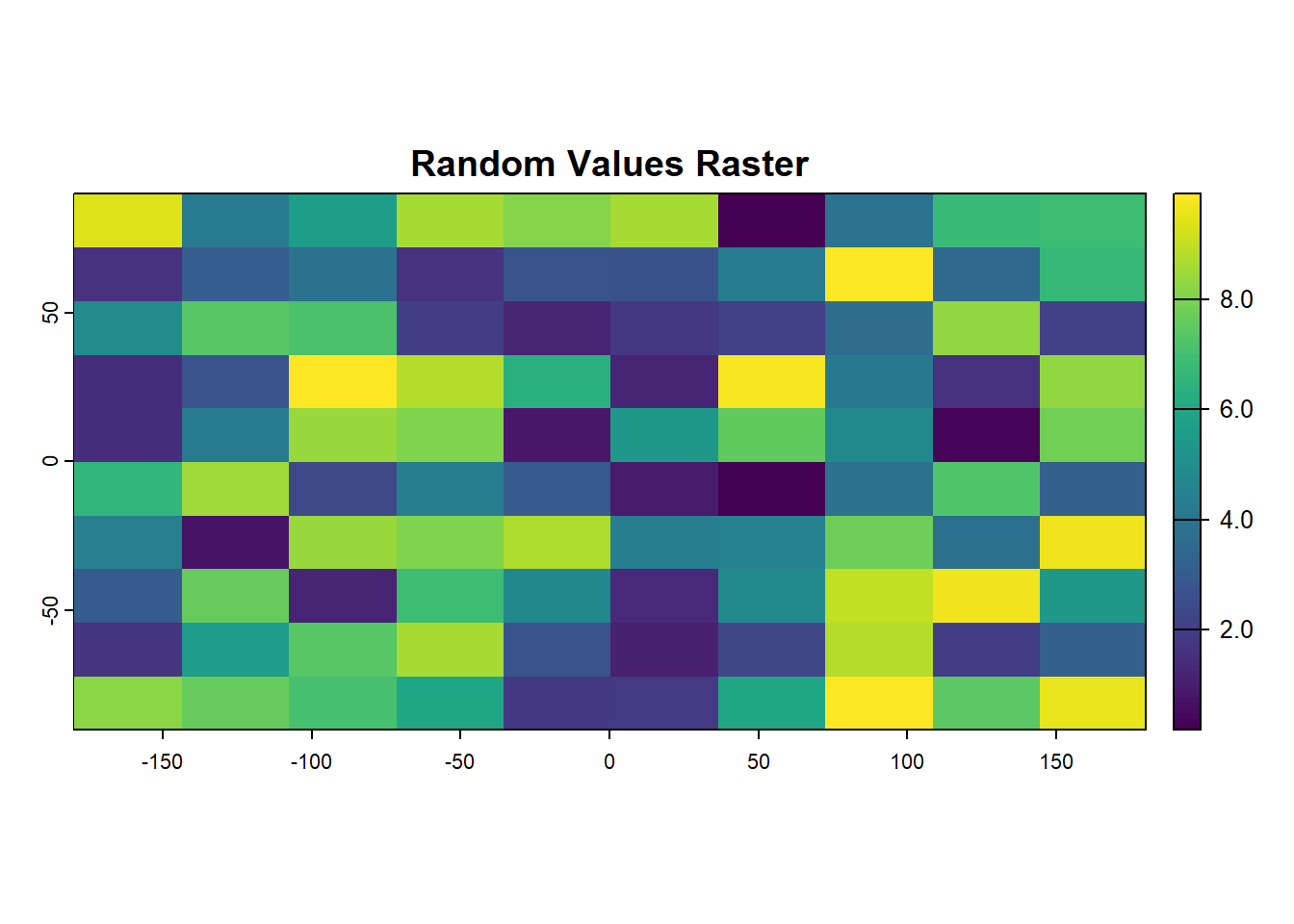
To create an empty SpatRaster object with 10 columns and 10 rows, assign random values between 0 and 10, and then plot it, you can use the terra package in R. Here’s how you can do it:

Code 
library(terra)

# Create an empty SpatRaster object with 10 columns and 10 rows
my_raster <- rast(nrows = 10, ncols = 10)

# Assign random values between 0 and 10
values(my_raster) <- runif(ncell(my_raster), min = 0, max = 10)

# Plot the raster
plot(my_raster, main = "Random Values Raster")

E5

To read in the raster/nlcd.tif file from the spDataLarge package and examine its properties, you can follow these steps in R:

library(spDataLarge)
library(terra)

# Read the raster file
nlcd_raster <- rast(system.file("raster/nlcd.tif", package = "spDataLarge"))

Information You Can Obtain: —

  1. Basic Properties: The print(nlcd_raster) command will provide you with information about the raster, including its dimensions, number of layers, and type of data.

    # Check the basic properties of the raster
print(nlcd_raster)
    class       : SpatRaster 
dimensions  : 1359, 1073, 1  (nrow, ncol, nlyr)
resolution  : 31.5303, 31.52466  (x, y)
extent      : 301903.3, 335735.4, 4111244, 4154086  (xmin, xmax, ymin, ymax)
coord. ref. : NAD83 / UTM zone 12N (EPSG:26912) 
source      : nlcd.tif 
color table : 1 
categories  : levels 
name        :   levels 
min value   :    Water 
max value   : Wetlands

  2. Summary Statistics: The summary(nlcd_raster) function will give you basic statistics about the raster values, such as minimum, maximum, and mean values. In this case, it tells the number of cells with Forest, Shrubland, Barren, Developed, Cultivated, Wetlands and Other land-use types.

    # Get summary statistics
summary(nlcd_raster)
            levels     
 Forest    :52620  
 Shrubland :37463  
 Barren    : 7290  
 Developed : 1203  
 Cultivated:  596  
 Wetlands  :  443  
 (Other)   :  421

  3. Extent: The ext(nlcd_raster) command will provide the geographical extent of the raster, showing the minimum and maximum x and y coordinates.

    # Check the extent of the raster
ext(nlcd_raster)
    SpatExtent : 301903.344386758, 335735.354381954, 4111244.46098842, 4154086.47216415 (xmin, xmax, ymin, ymax)

  4. Rows and Columns: You can find the number of rows and columns in the raster using nrow(nlcd_raster) and ncol(nlcd_raster).

    # Get the number of rows and columns
nrow(nlcd_raster)
    [1] 1359
    ncol(nlcd_raster)
    [1] 1073

  5. Coordinate Reference System (CRS): The crs(nlcd_raster) command will return the CRS of the raster, which is essential for spatial analyses.

    # Get the coordinate reference system (CRS)
str_view(crs(nlcd_raster))
    [1] │ PROJCRS["NAD83 / UTM zone 12N",
    │     BASEGEOGCRS["NAD83",
    │         DATUM["North American Datum 1983",
    │             ELLIPSOID["GRS 1980",6378137,298.257222101,
    │                 LENGTHUNIT["metre",1]]],
    │         PRIMEM["Greenwich",0,
    │             ANGLEUNIT["degree",0.0174532925199433]],
    │         ID["EPSG",4269]],
    │     CONVERSION["UTM zone 12N",
    │         METHOD["Transverse Mercator",
    │             ID["EPSG",9807]],
    │         PARAMETER["Latitude of natural origin",0,
    │             ANGLEUNIT["degree",0.0174532925199433],
    │             ID["EPSG",8801]],
    │         PARAMETER["Longitude of natural origin",-111,
    │             ANGLEUNIT["degree",0.0174532925199433],
    │             ID["EPSG",8802]],
    │         PARAMETER["Scale factor at natural origin",0.9996,
    │             SCALEUNIT["unity",1],
    │             ID["EPSG",8805]],
    │         PARAMETER["False easting",500000,
    │             LENGTHUNIT["metre",1],
    │             ID["EPSG",8806]],
    │         PARAMETER["False northing",0,
    │             LENGTHUNIT["metre",1],
    │             ID["EPSG",8807]]],
    │     CS[Cartesian,2],
    │         AXIS["(E)",east,
    │             ORDER[1],
    │             LENGTHUNIT["metre",1]],
    │         AXIS["(N)",north,
    │             ORDER[2],
    │             LENGTHUNIT["metre",1]],
    │     USAGE[
    │         SCOPE["Engineering survey, topographic mapping."],
    │         AREA["North America - between 114°W and 108°W - onshore and offshore. Canada - Alberta; Northwest Territories; Nunavut; Saskatchewan. United States (USA) - Arizona; Colorado; Idaho; Montana; New Mexico; Utah; Wyoming."],
    │         BBOX[31.33,-114,84,-108]],
    │     ID["EPSG",26912]]

  6. Resolution: You can check the resolution of the raster with the res(nlcd_raster) function, which will indicate the size of each pixel.

    # Check the resolution of the raster
res(nlcd_raster)
    [1] 31.53030 31.52466

  7. Values: The values(nlcd_raster) command allows you to access the actual values contained in the raster. Here, I am printing only the first few values.

    # Get the values of the raster
values(nlcd_raster) |> head()
         levels
[1,]      4
[2,]      4
[3,]      5
[4,]      4
[5,]      4
[6,]      4

E6

To check the Coordinate Reference System (CRS) of the raster/nlcd.tif file from the spDataLarge package, you can use the following steps in R. The CRS provides essential information about how the spatial data is projected on the Earth’s surface.

library(spDataLarge)
library(terra)

# Read the raster file
nlcd_raster <- rast(system.file("raster/nlcd.tif", package = "spDataLarge"))

# Check the coordinate reference system (CRS)
nlcd_crs <- crs(nlcd_raster)
nlcd_crs |> str_view()
[1] │ PROJCRS["NAD83 / UTM zone 12N",
    │     BASEGEOGCRS["NAD83",
    │         DATUM["North American Datum 1983",
    │             ELLIPSOID["GRS 1980",6378137,298.257222101,
    │                 LENGTHUNIT["metre",1]]],
    │         PRIMEM["Greenwich",0,
    │             ANGLEUNIT["degree",0.0174532925199433]],
    │         ID["EPSG",4269]],
    │     CONVERSION["UTM zone 12N",
    │         METHOD["Transverse Mercator",
    │             ID["EPSG",9807]],
    │         PARAMETER["Latitude of natural origin",0,
    │             ANGLEUNIT["degree",0.0174532925199433],
    │             ID["EPSG",8801]],
    │         PARAMETER["Longitude of natural origin",-111,
    │             ANGLEUNIT["degree",0.0174532925199433],
    │             ID["EPSG",8802]],
    │         PARAMETER["Scale factor at natural origin",0.9996,
    │             SCALEUNIT["unity",1],
    │             ID["EPSG",8805]],
    │         PARAMETER["False easting",500000,
    │             LENGTHUNIT["metre",1],
    │             ID["EPSG",8806]],
    │         PARAMETER["False northing",0,
    │             LENGTHUNIT["metre",1],
    │             ID["EPSG",8807]]],
    │     CS[Cartesian,2],
    │         AXIS["(E)",east,
    │             ORDER[1],
    │             LENGTHUNIT["metre",1]],
    │         AXIS["(N)",north,
    │             ORDER[2],
    │             LENGTHUNIT["metre",1]],
    │     USAGE[
    │         SCOPE["Engineering survey, topographic mapping."],
    │         AREA["North America - between 114°W and 108°W - onshore and offshore. Canada - Alberta; Northwest Territories; Nunavut; Saskatchewan. United States (USA) - Arizona; Colorado; Idaho; Montana; New Mexico; Utah; Wyoming."],
    │         BBOX[31.33,-114,84,-108]],
    │     ID["EPSG",26912]]

Understanding the CRS Information: —

The output from the crs(nlcd_raster) command will typically include details such as:

  1. Projection Type: Indicates whether the CRS is geographic (latitude and longitude) or projected (a flat representation). Here, it is North American NAD83 / UTM Zone 12 N

  2. Datum: Information about the geodetic datum used, which is crucial for accurately locating points on the Earth’s surface. Here, it is North American Datum 1983.

  3. Coordinate Units: Specifies the units of measurement used for the coordinates, such as degrees (for geographic CRSs) or meters (for projected CRSs). Here, it is in metres, as shown in:

    LENGTHUNIT["metre",1]

  4. EPSG Code: If applicable, the output might include an EPSG code, which is a standardized reference number for a specific CRS. This code can be used to look up more detailed information about the CRS. Here, it is: —

    ID["EPSG",26912]

  5. Transformation Parameters: If it’s a projected CRS, the output may include parameters related to the projection method, such as central meridian, standard parallels, and false easting/northing. Here, they are: —

    |         PRIMEM["Greenwich",0,     
│             ANGLEUNIT["degree",0.0174532925199433]],     
│         ID["EPSG",4269]], 
|
|
│     CONVERSION["UTM zone 12N",     
│         METHOD["Transverse Mercator",     
│             ID["EPSG",9807]],     
│         PARAMETER["Latitude of natural origin",0,     
│             ANGLEUNIT["degree",0.0174532925199433],     
│             ID["EPSG",8801]],     
│         PARAMETER["Longitude of natural origin",-111,     
|             ANGLEUNIT["degree",0.0174532925199433],     
│             ID["EPSG",8802]],     
│         PARAMETER["Scale factor at natural origin",0.9996,
│             SCALEUNIT["unity",1],     
│             ID["EPSG",8805]],     
│         PARAMETER["False easting",500000,     
│             LENGTHUNIT["metre",1],     
│             ID["EPSG",8806]],     
│         PARAMETER["False northing",0,     
│             LENGTHUNIT["metre",1],     
│             ID["EPSG",8807]]],

References

Cooley, David. 2024. “Sfheaders: Converts Between r Objects and Simple Feature Objects.” https://CRAN.R-project.org/package=sfheaders.
Oscar Perpiñán, and Robert Hijmans. 2023. “rasterVis.” https://oscarperpinan.github.io/rastervis/.
Tennekes, Martijn. 2018. “Tmap: Thematic Maps in r” 84. https://doi.org/10.18637/jss.v084.i06.