Chapter 15

Coordinate Systems

Author

Aditya Dahiya

Published

March 4, 2024

This chapter has no exercises, so I use a dummy dataset to generate some examples of the functions and ggplot2 customization of coordinates discussed in this chapter.

Code

To begin with, lets create a dummy data set shown in Figure 1

Code
set.seed(123)
tb <- tibble(
  v_integer = 1:20,
  v_squared = v_integer ^ 2,
  v_regress = round(
    (v_integer ^ 2) + 
      rnorm(
        20, mean = 0, sd = 1), 
    2),
  v_random = sample(1:100, 20, replace = FALSE),
  v_discrete = sample(LETTERS[1:4], 20, replace = TRUE)
)
tb |> 
  gt() |> 
  cols_align("center") |> 
  gt_theme_538()
v_integer v_squared v_regress v_random v_discrete
1 1 0.44 15 B
2 4 3.77 32 A
3 9 10.56 7 A
4 16 16.07 9 C
5 25 25.13 41 A
6 36 37.72 74 B
7 49 49.46 23 A
8 64 62.73 27 C
9 81 80.31 60 A
10 100 99.55 53 C
11 121 122.22 98 B
12 144 144.36 91 D
13 169 169.40 93 C
14 196 196.11 38 D
15 225 224.44 34 D
16 256 257.79 69 B
17 289 289.50 72 B
18 324 322.03 76 C
19 361 361.70 63 D
20 400 399.53 13 B
Figure 1: A dummy dataset to use in the examples for this Chapters’ Solutions / Examples

15.1 Linear coordinate systems

Let’s use the example plot in Figure 2 to demonstrate the various changes / customization possible with ggplot2 with coordinates.

Code
g1 <- tb |>
  ggplot(
    aes(
      x = v_integer,
      y = v_regress
    )
  ) +
  geom_smooth(
    se = TRUE,
    colour = "grey",
    fill = "lightgrey",
    alpha = 0.5
  ) +
  geom_point(
    aes(colour = v_discrete),
    size = 3
  ) +
  scale_colour_brewer(palette = "Dark2") +
  theme_minimal() +
  theme(axis.line = element_line(arrow = arrow()))
g1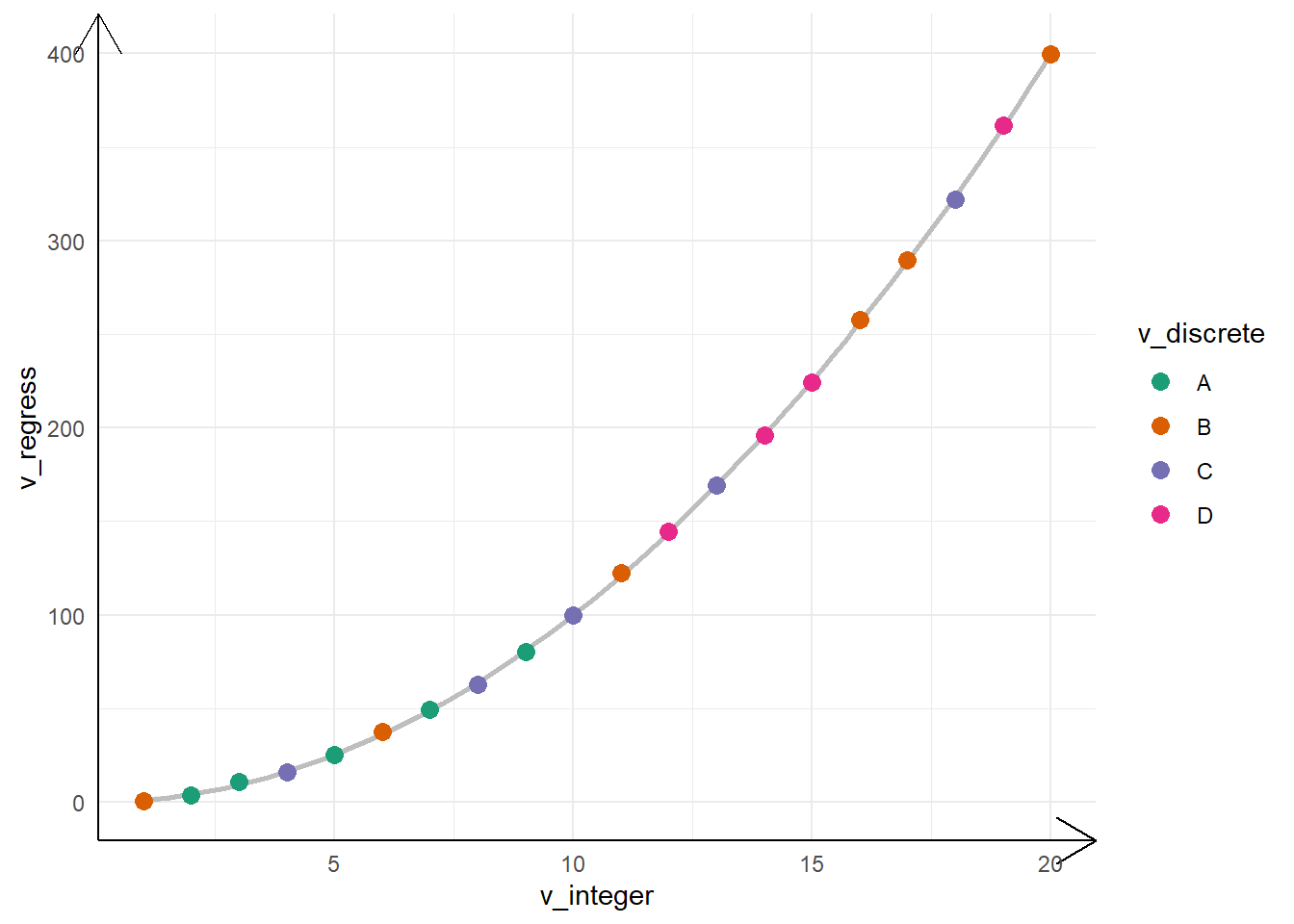
Figure 2: An example plot which we will later use in various examples of tweaking the Linear Coordinate Systems

15.1.1 Zooming into a plot with coord_cartesian()

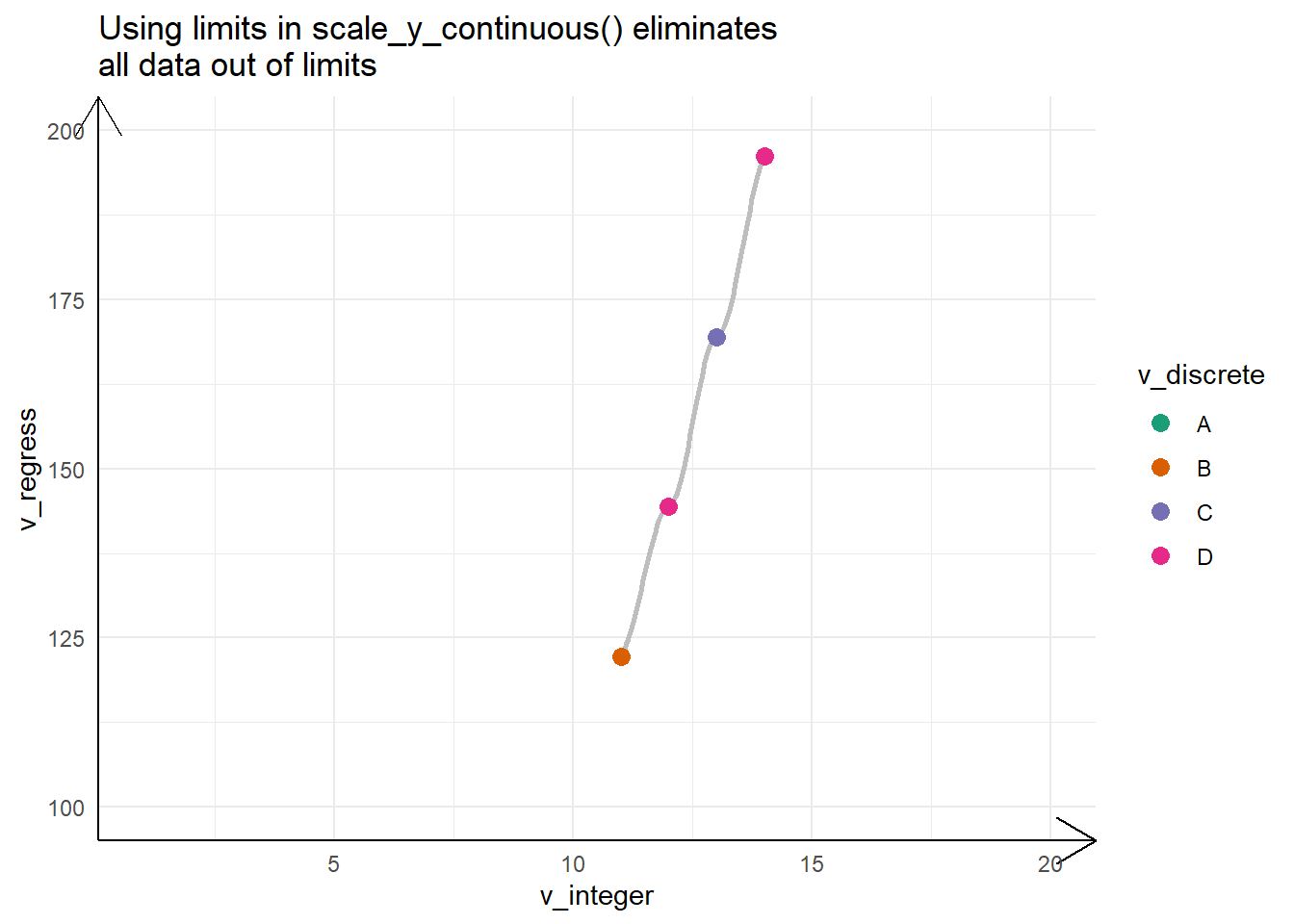
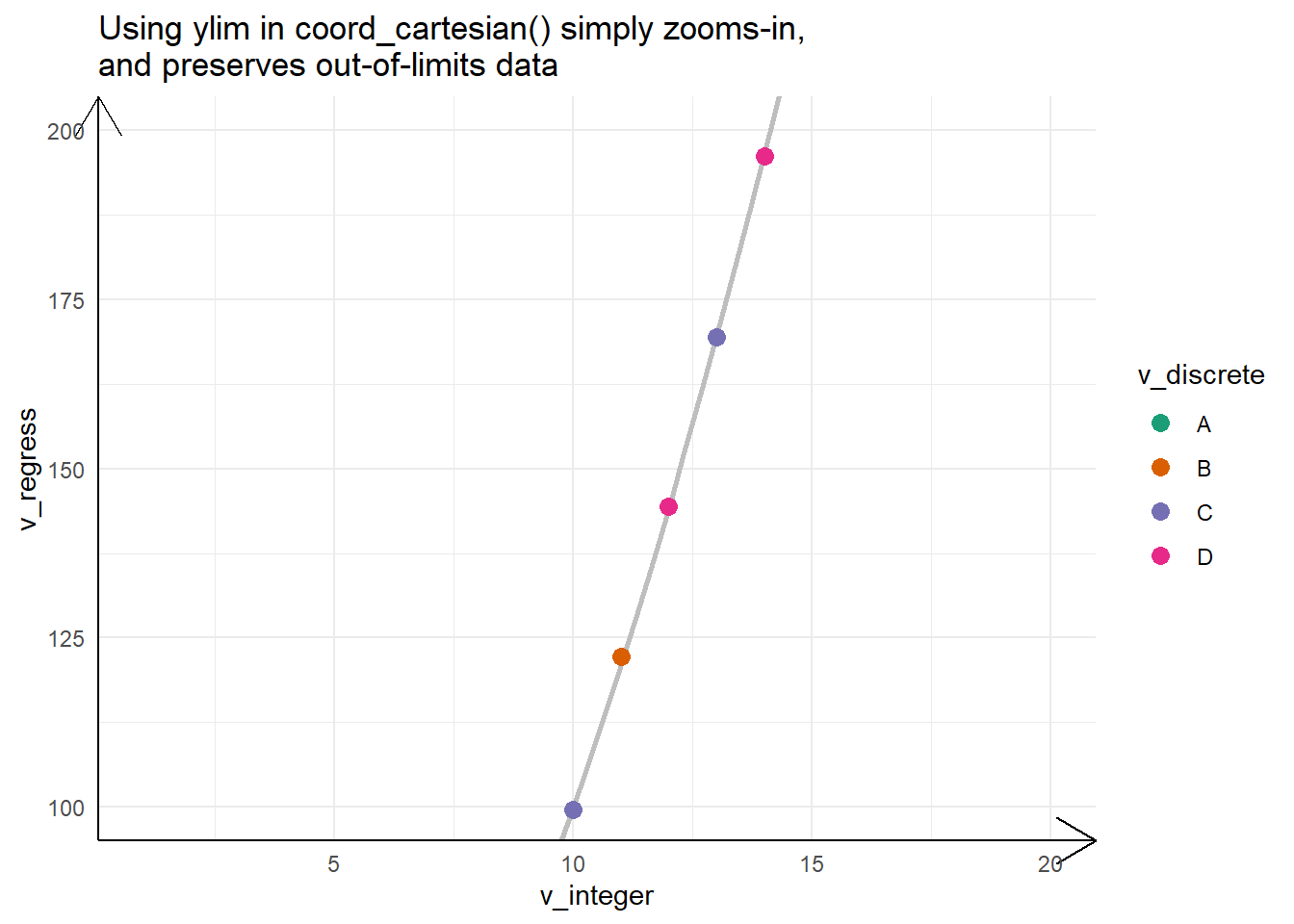
The Figure 3 shows an example of zooming into a plot with coord_cartesian() and its difference from the other option using scale_*_continuous(limits = *) .

Code
g1 +
  labs(title = "The Base Plot shows entire data")

g1 + scale_y_continuous(limits = c(100, 200)) +
  labs(title = "Using limits in scale_y_continuous() eliminates\nall data out of limits")

g1 + coord_cartesian(ylim = c(100, 200)) +
  labs(title = "Using ylim in coord_cartesian() simply zooms-in,\nand preserves out-of-limits data")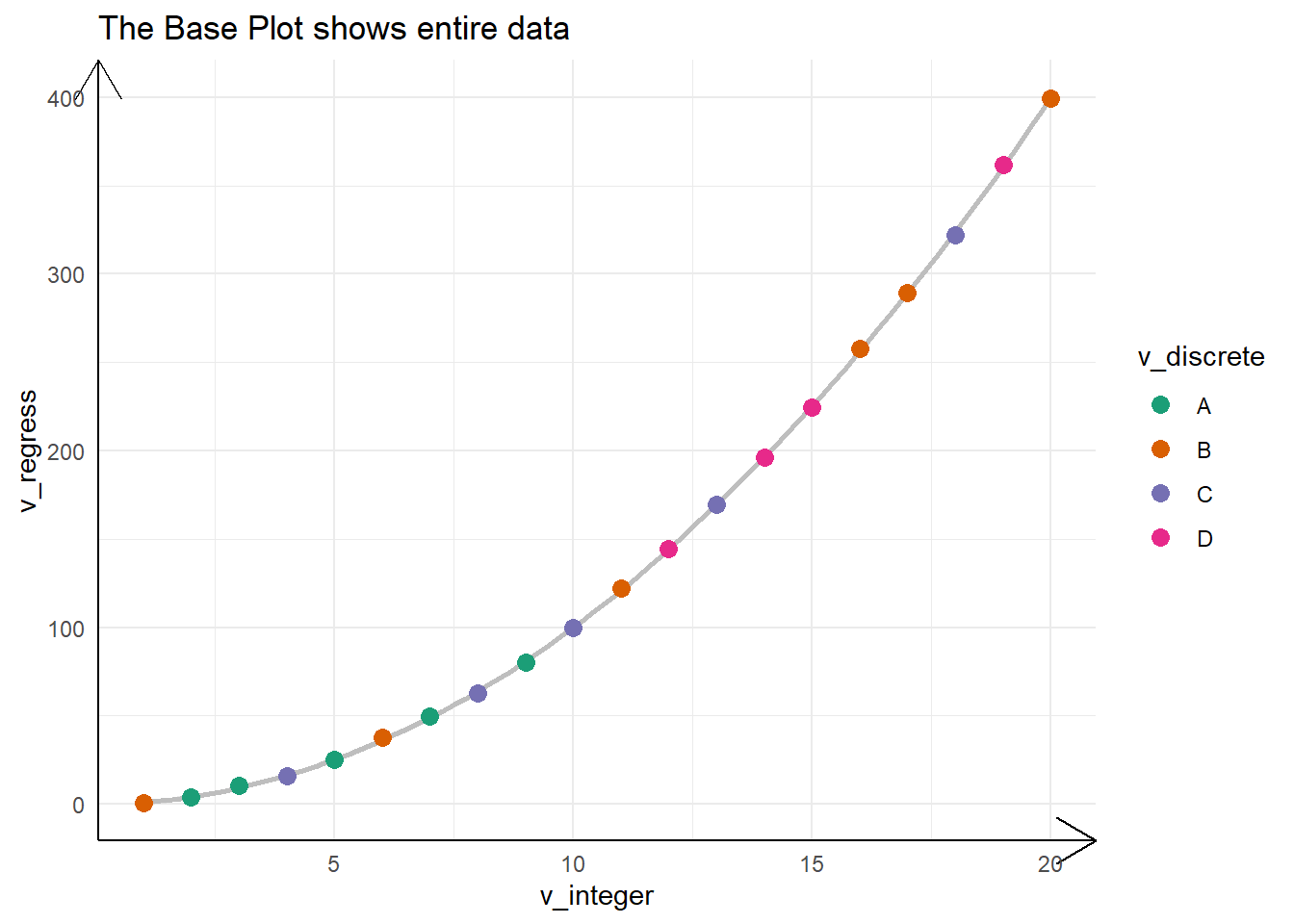
(a) Base Plot
(b) Limits argument in scale_y_continuous()
(c) ylim argument in coord_cartesian()
Figure 3: Zooming in on a specified portion of Y-Axis: 100 to 200

15.1.2 Flipping the axes with coord_flip()

The Figure 4 shows examples of flipping the coordinates, and reasoning as to why it may be better than changing X-axis and Y-axis variables manually, especially if we are using geom_smooth() which uses y ~ x formula by default.

Code
g1 + labs(title = "The base plot",
                subtitle = "Dependent variable is v_regress, and independent var is v_integer")

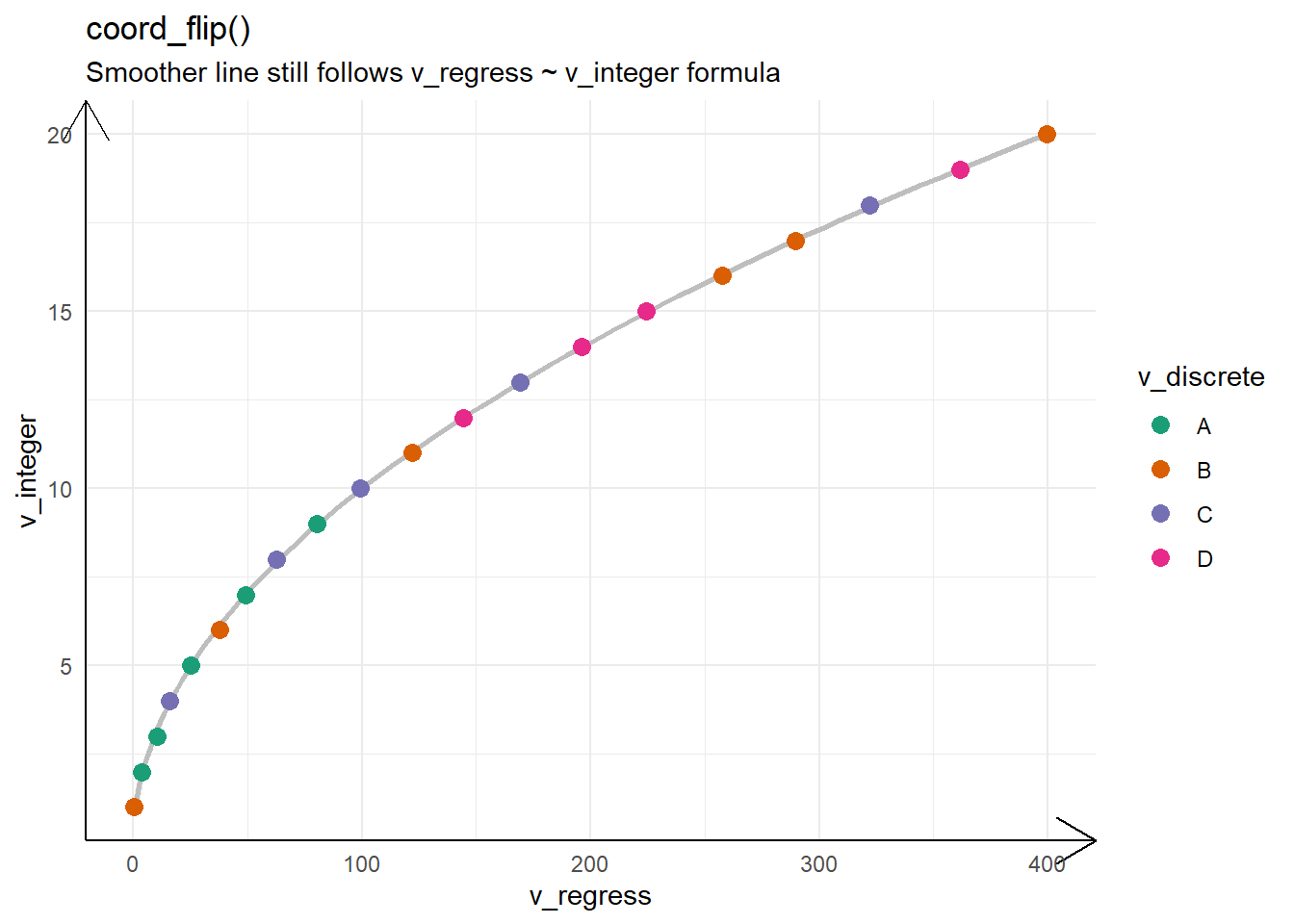
g1 + 
  coord_flip() +
  labs(title = "coord_flip()",
       subtitle = "Smoother line still follows v_regress ~ v_integer formula")

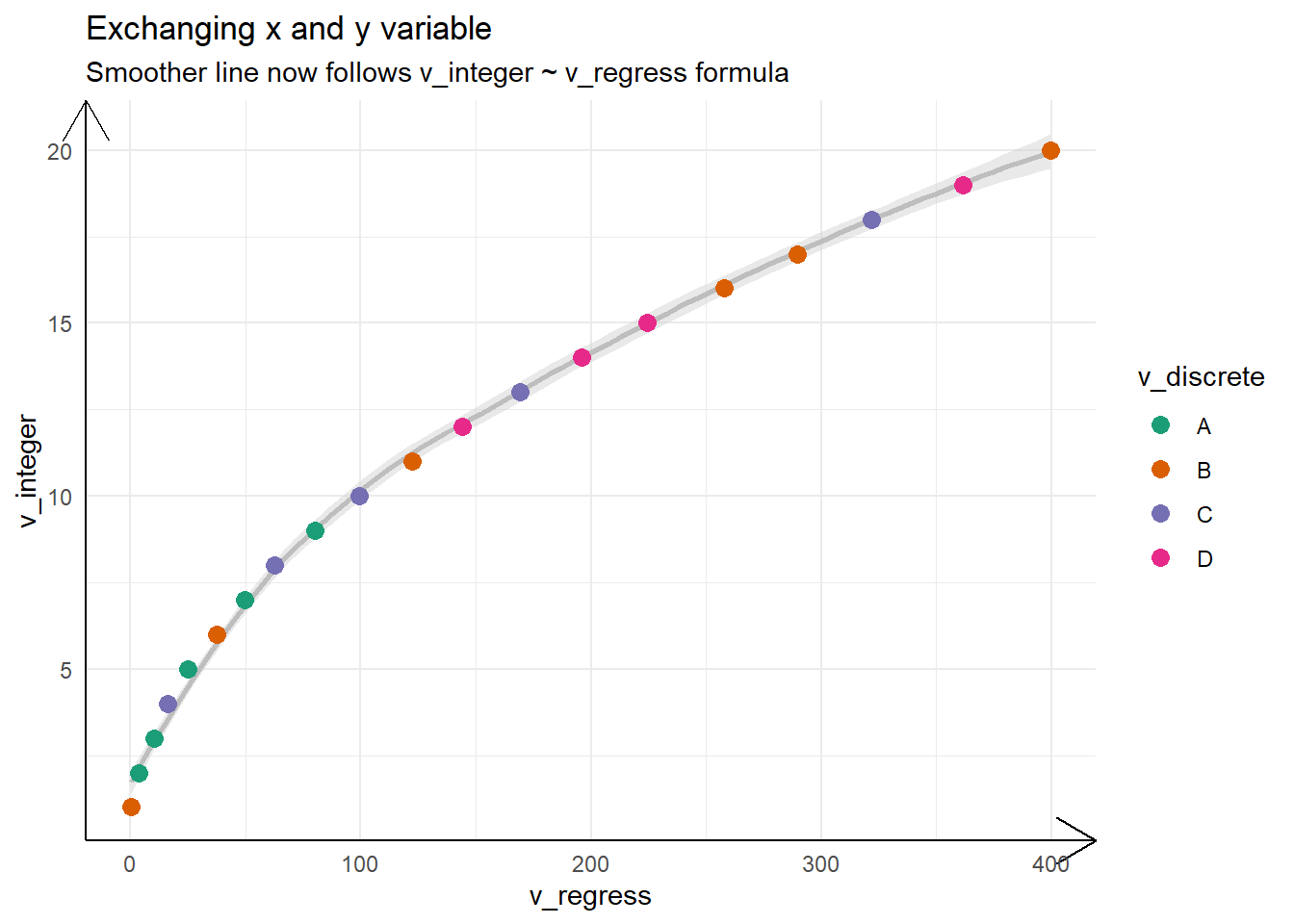
tb |>
  ggplot(
    aes(
      y = v_integer,
      x = v_regress
    )
  ) +
  geom_smooth(
    se = TRUE,
    colour = "grey",
    fill = "lightgrey",
    alpha = 0.5
  ) +
  geom_point(
    aes(colour = v_discrete),
    size = 3
  ) +
  scale_color_brewer(palette = "Dark2") +
  theme_minimal() +
  theme(axis.line = element_line(arrow = arrow())) + 
  labs(title = "Exchanging x and y variable",
       subtitle = "Smoother line now follows v_integer ~ v_regress formula")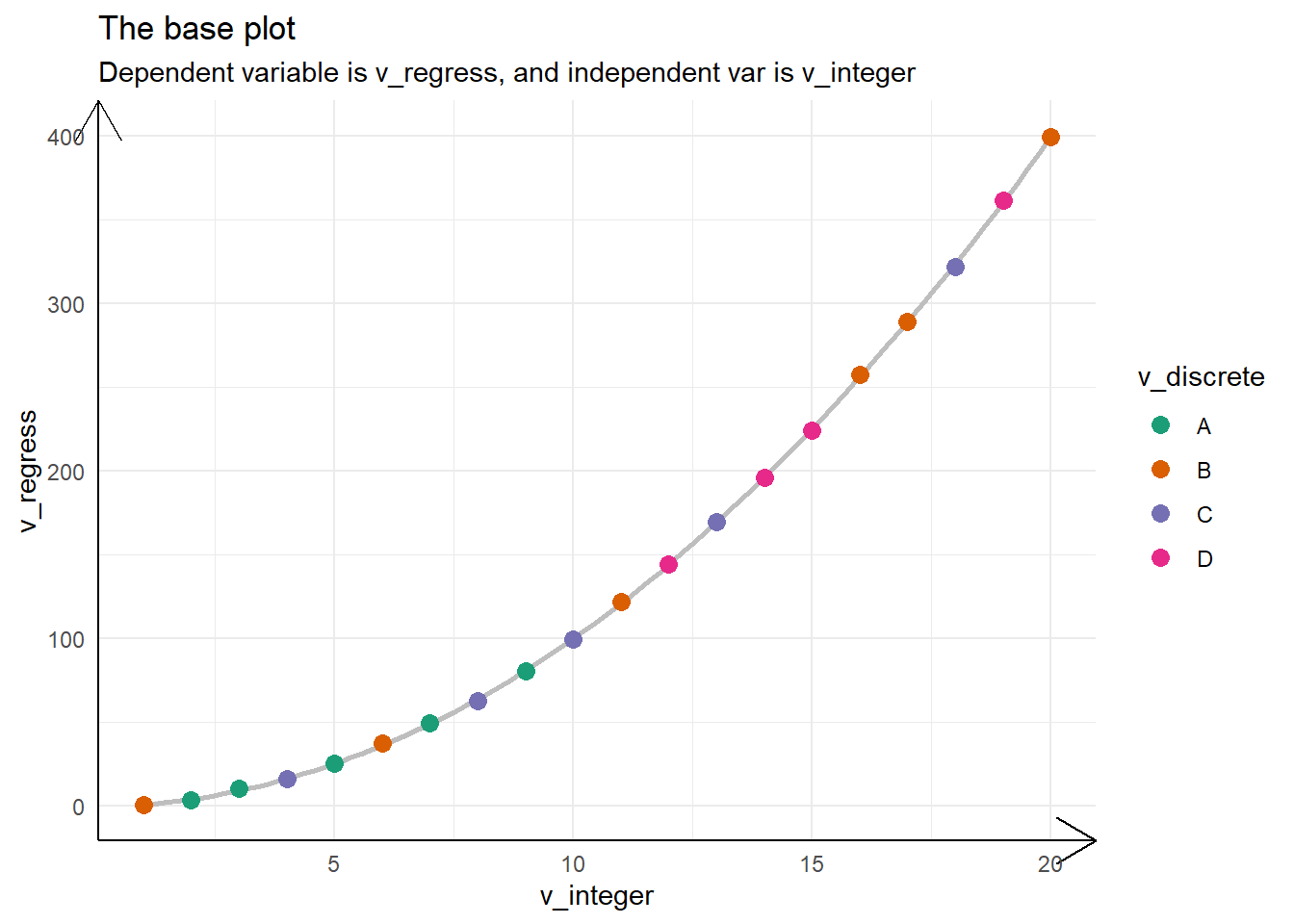
(a) The base plot
(b) Smoother line still follows v_regress ~ v_integer formula
(c) Smoother line now follows v_integer ~ v_regress formula
Figure 4: Demonstrating the use of coord_flip()

15.1.3 Equal scales with coord_fixed()

The Figure 5 shows the same three graphs above, but in a much better sense now that coordinates are fixed to be equal.

Code
g1 + labs(title = "The base plot")

g1 + coord_fixed() + labs(title = "The base plot with coord_fixed()")
(a) The base plot
(b) The base plot with fixed coordinates
Figure 5: Demonstrating the use of coord_fixed()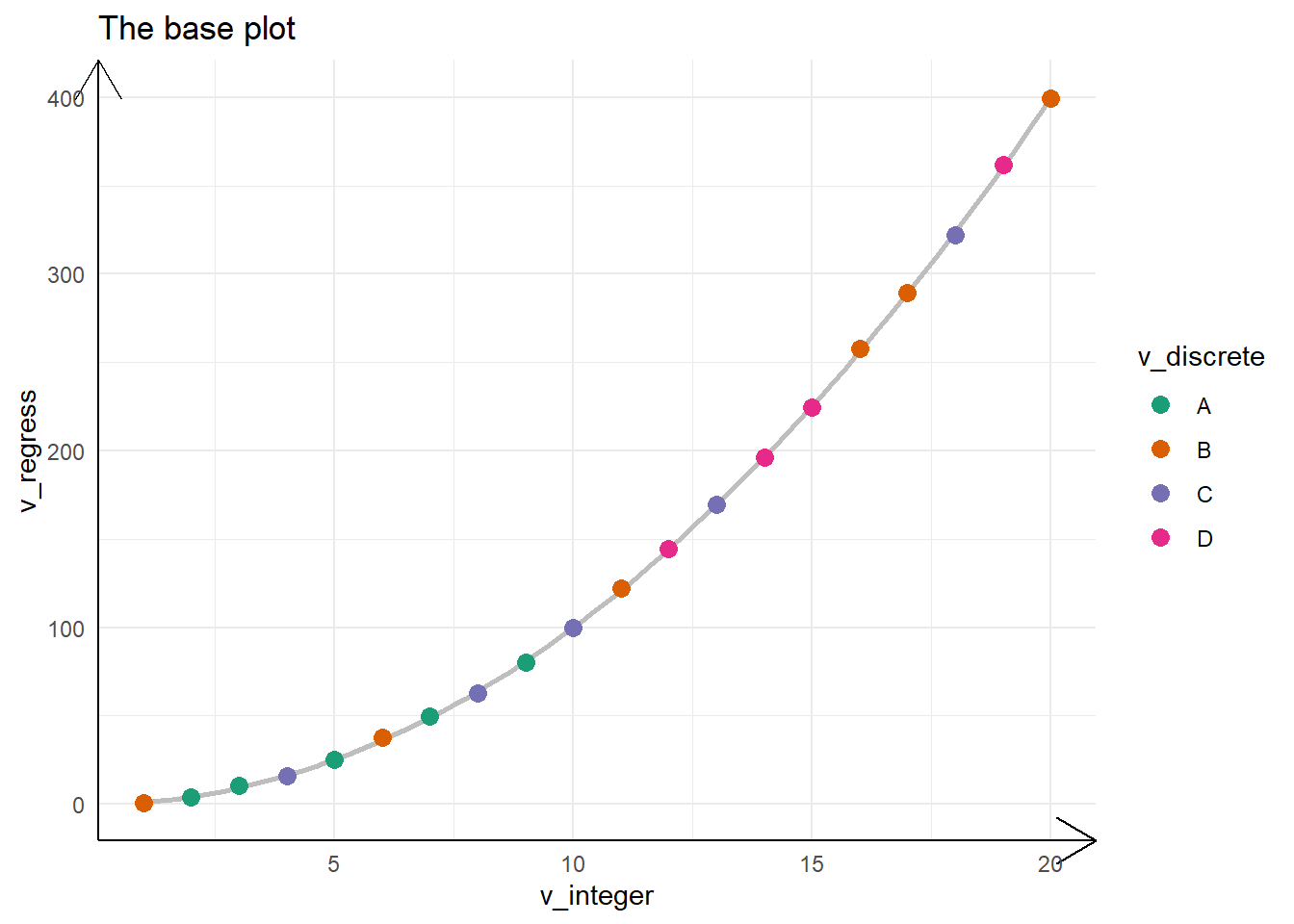

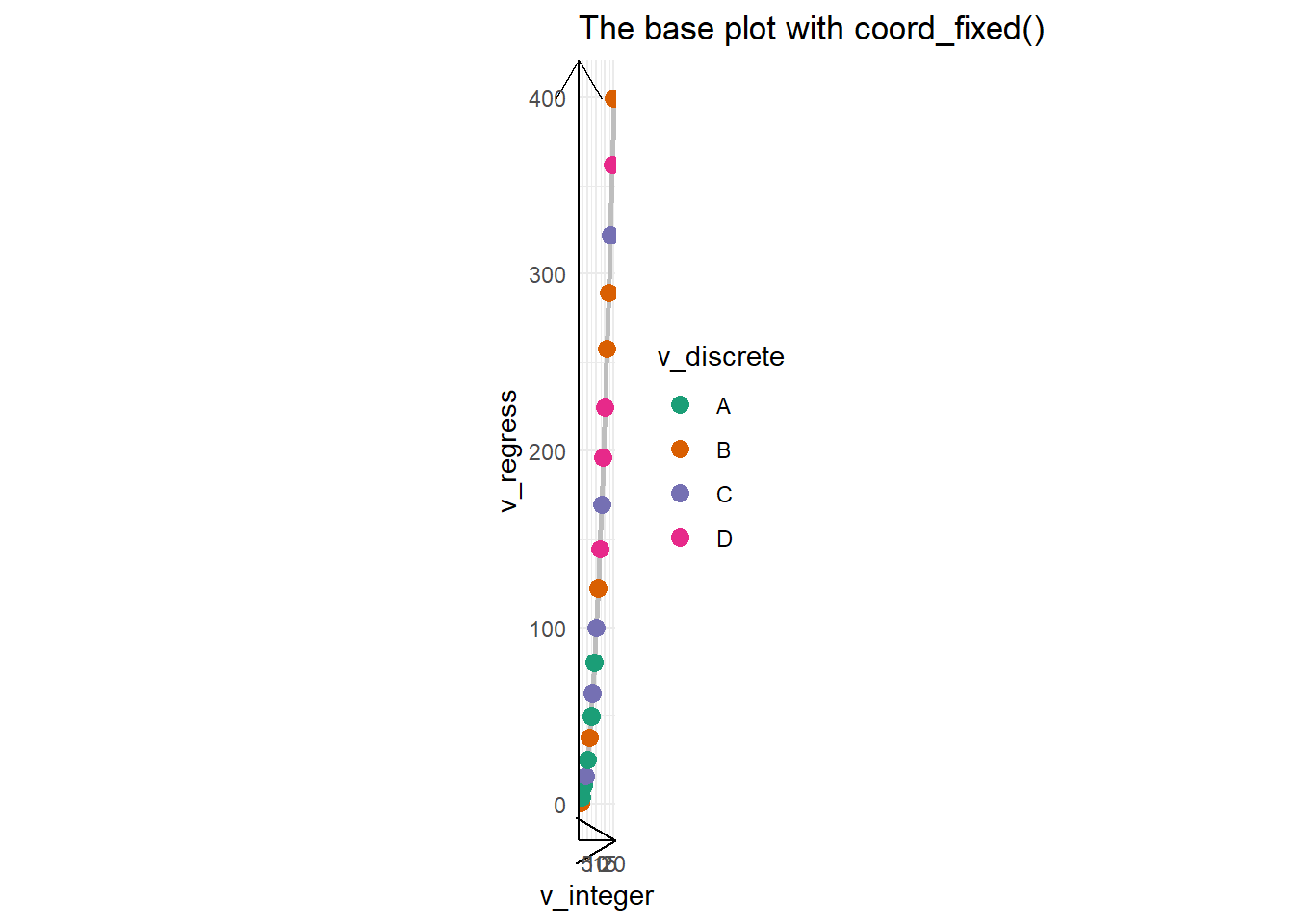
15.2 Non-linear coordinate systems

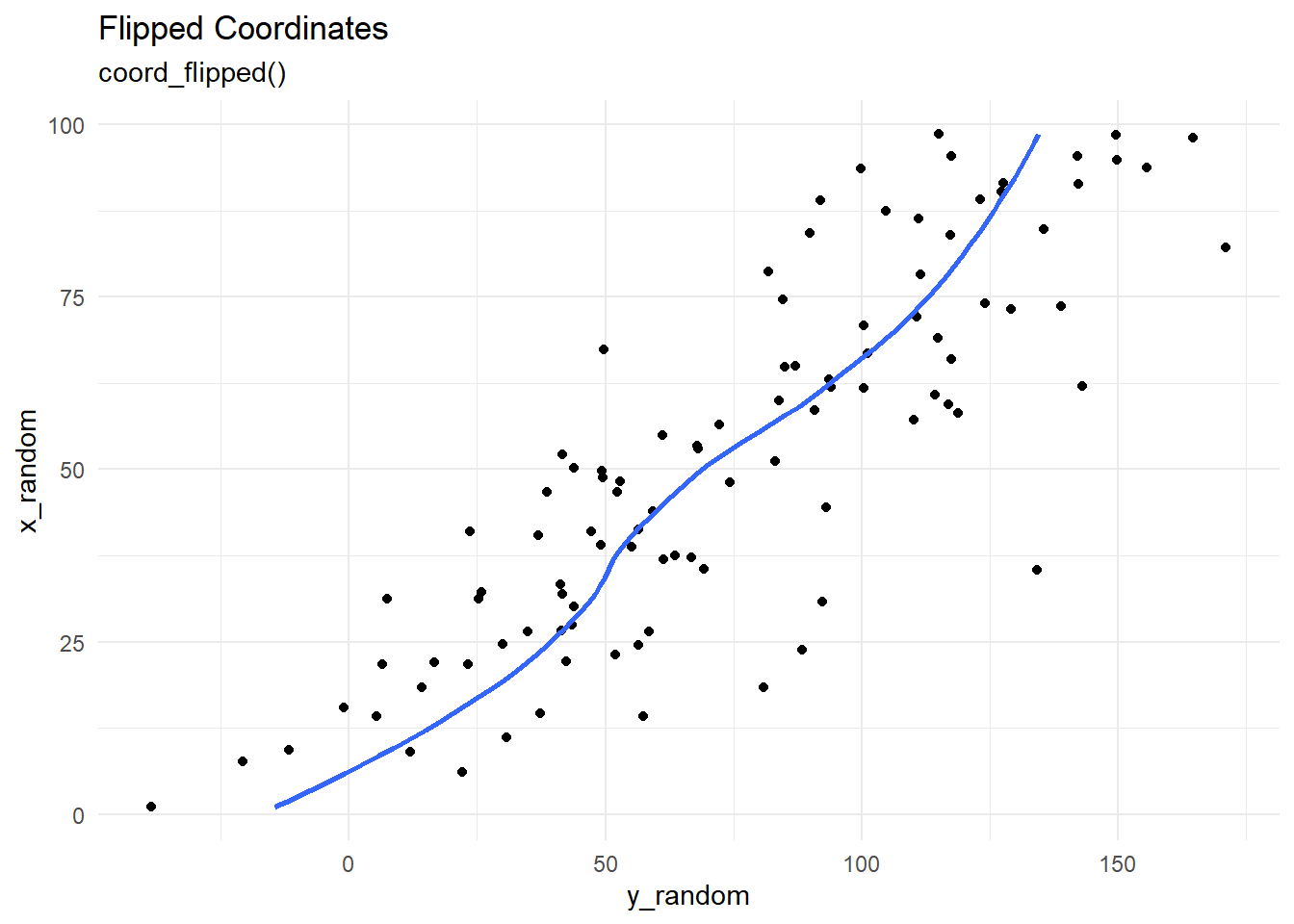
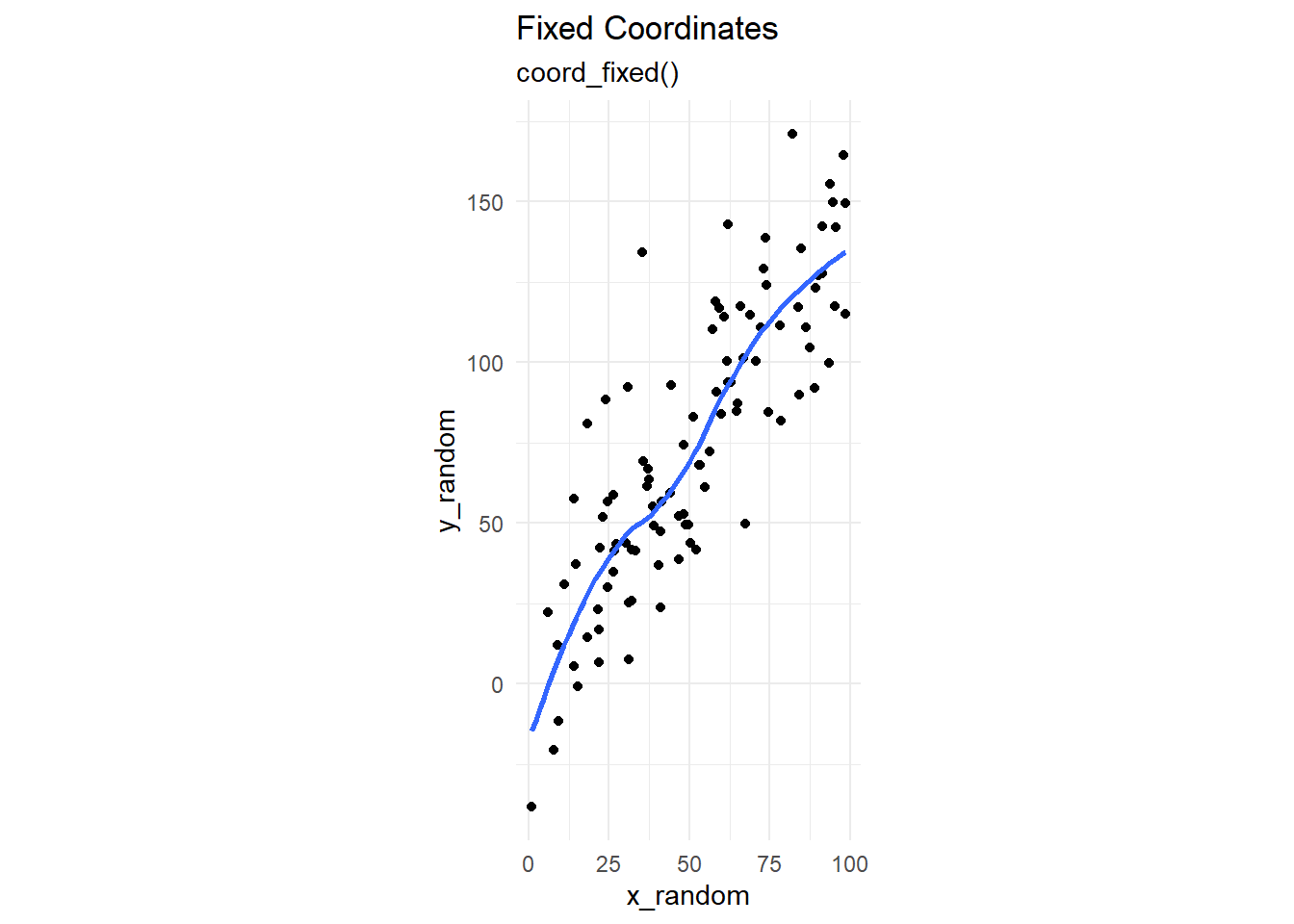
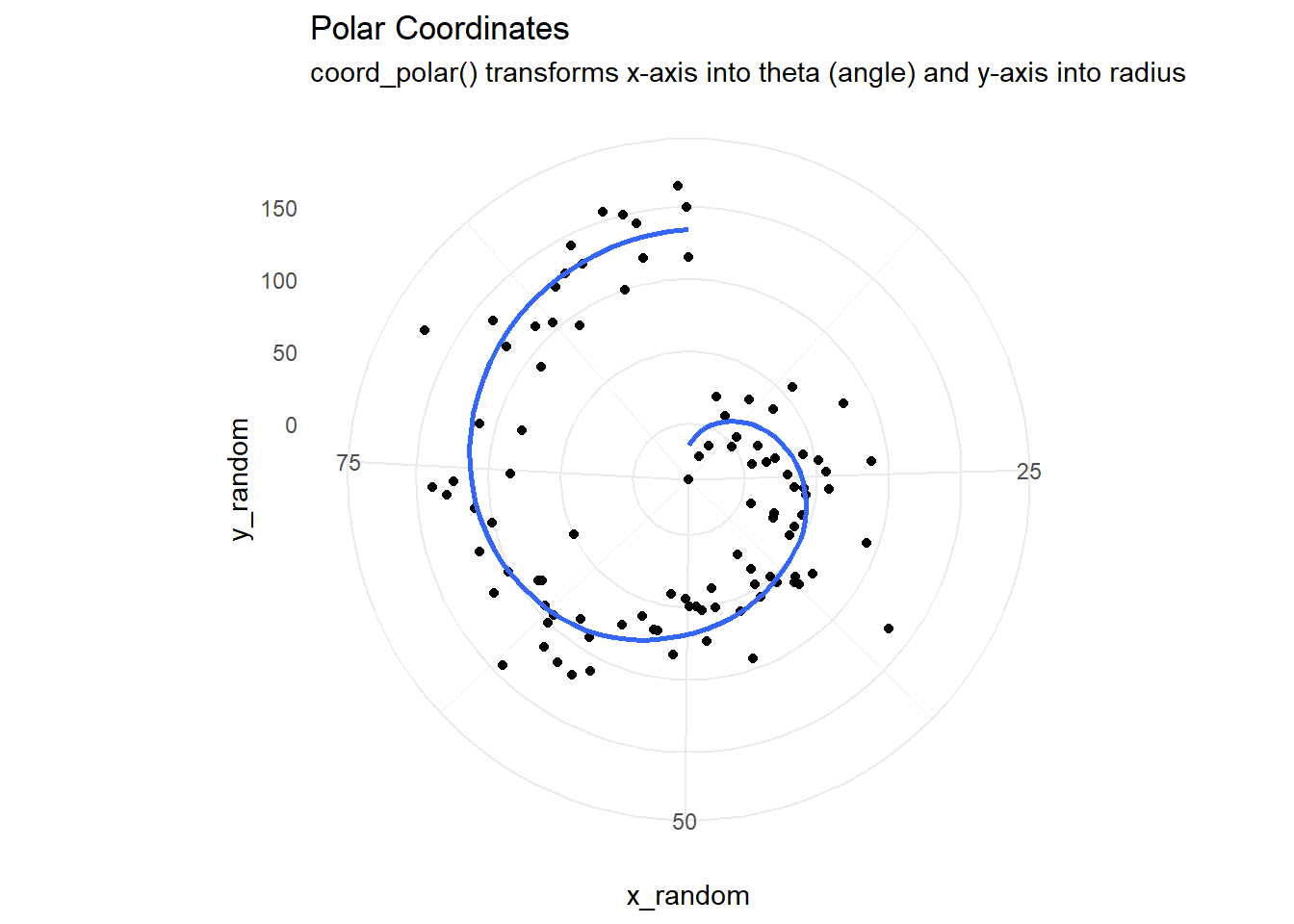
The Figure 6 demonstrates five types of coordinate systems - first three linear, and the last two non-linear.

Code
tb <- tibble(
  x_random = runif(100, min = 0, max = 100),
  y_random = (1.5 * x_random) + (rnorm(100, 0, 25))
)

g1 <- ggplot(tb, aes(x_random, y_random)) +
  geom_point() +
  geom_smooth(se = FALSE) +
  labs(title = "Cartesian Coordinates") +
  theme_minimal()

g1 

g1 + coord_flip() + 
  labs(title = "Flipped Coordinates",
       subtitle = "coord_flipped()")

g1 + coord_fixed() +
  labs(title = "Fixed Coordinates",
       subtitle = "coord_fixed()")

g1 + coord_polar() +
  labs(title = "Polar Coordinates",
       subtitle = "coord_polar() transforms x-axis into theta (angle) and y-axis into radius")

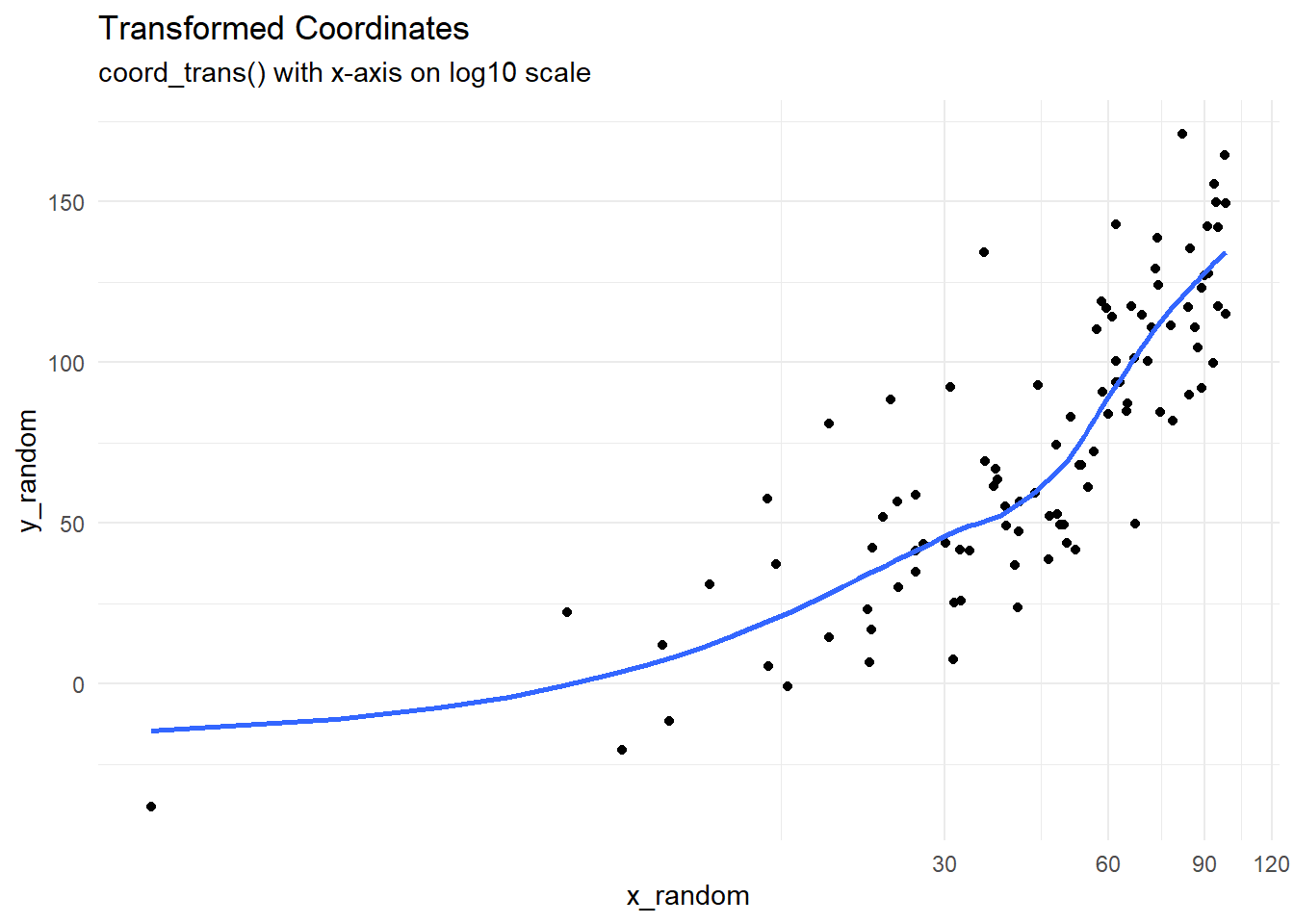
g1 + coord_trans(x = "log10") +
  labs(title = "Transformed Coordinates",
       subtitle = "coord_trans() with x-axis on log10 scale")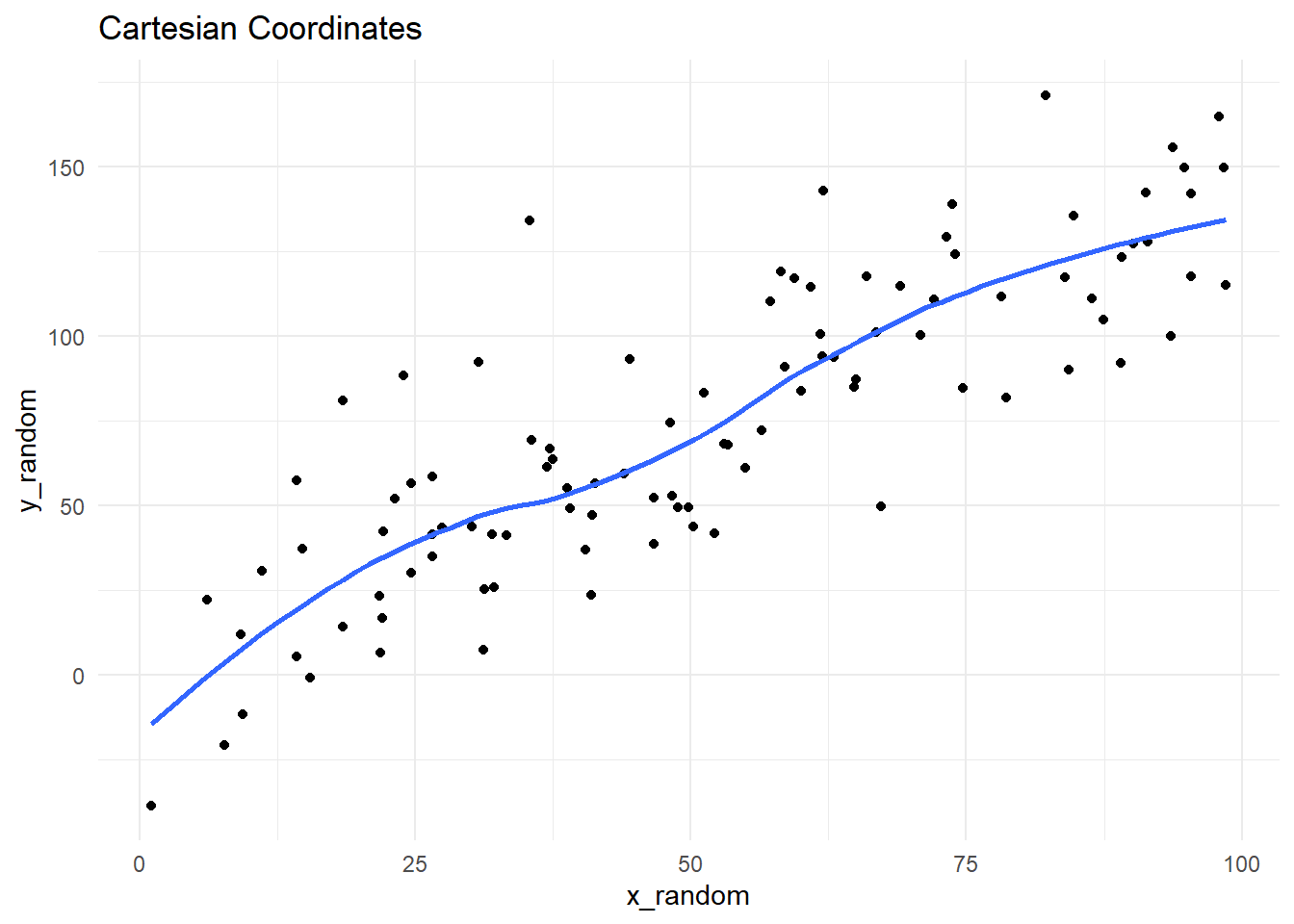
(a) coord_cartesian()
(b) coord_flip()
(c) coord_fixed()
(d) coord_polar()
(e) coord_trans()
Figure 6: A demonstration of Polar Coordinates, Flipped Coordinates, Transformed Coordinates and Fixed Coordinates

15.2.1 Transformations with coord_trans()

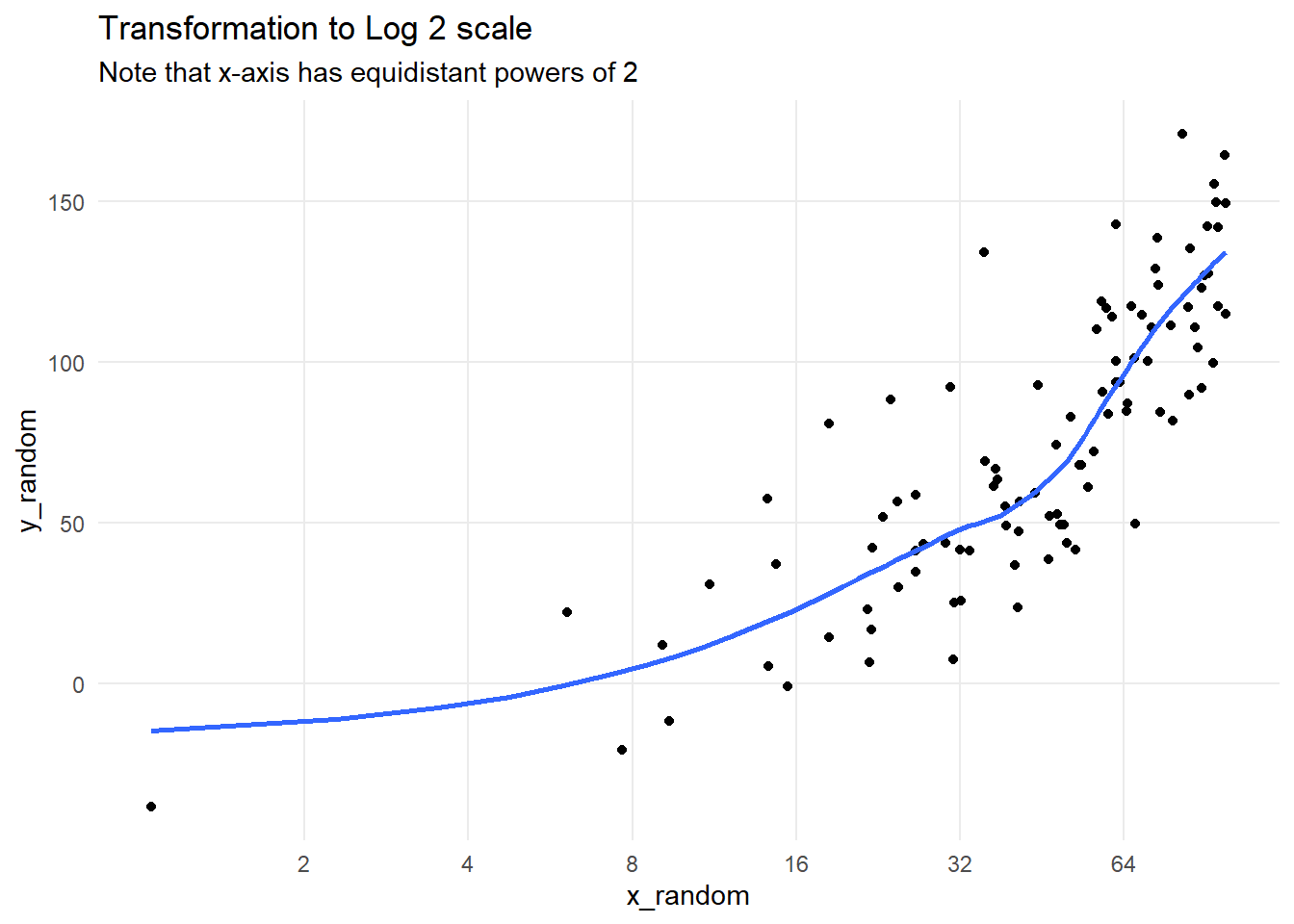
The impact of coord_trans() can be demonstrated in Figure 7 shown below.

Code
g1 +
  coord_trans(x = "log2") +
  scale_x_continuous(breaks = 2^(1:8)) +
  theme(panel.grid.minor = element_blank()) +
  labs(
    title = "Transformation to Log 2 scale",
    subtitle = "Note that x-axis has equidistant powers of 2"
  )
Figure 7: Use of coord_trans() to change the graph into a non-linear one

15.2.2 Polar coordinates with coord_polar()

The Figure 8 demonstrates various uses of coord_polar()

Code
tb2 <- tibble(
  Type = sample(LETTERS[1:4], size = 10, replace = T)
)

g2 <- tb2 |> 
  ggplot(aes(x = "1", fill = Type)) +
  geom_bar() +
  labs(title = "A Stacked Bar-Chart") +
  theme_void() +
  theme(legend.position = "bottom")

g2


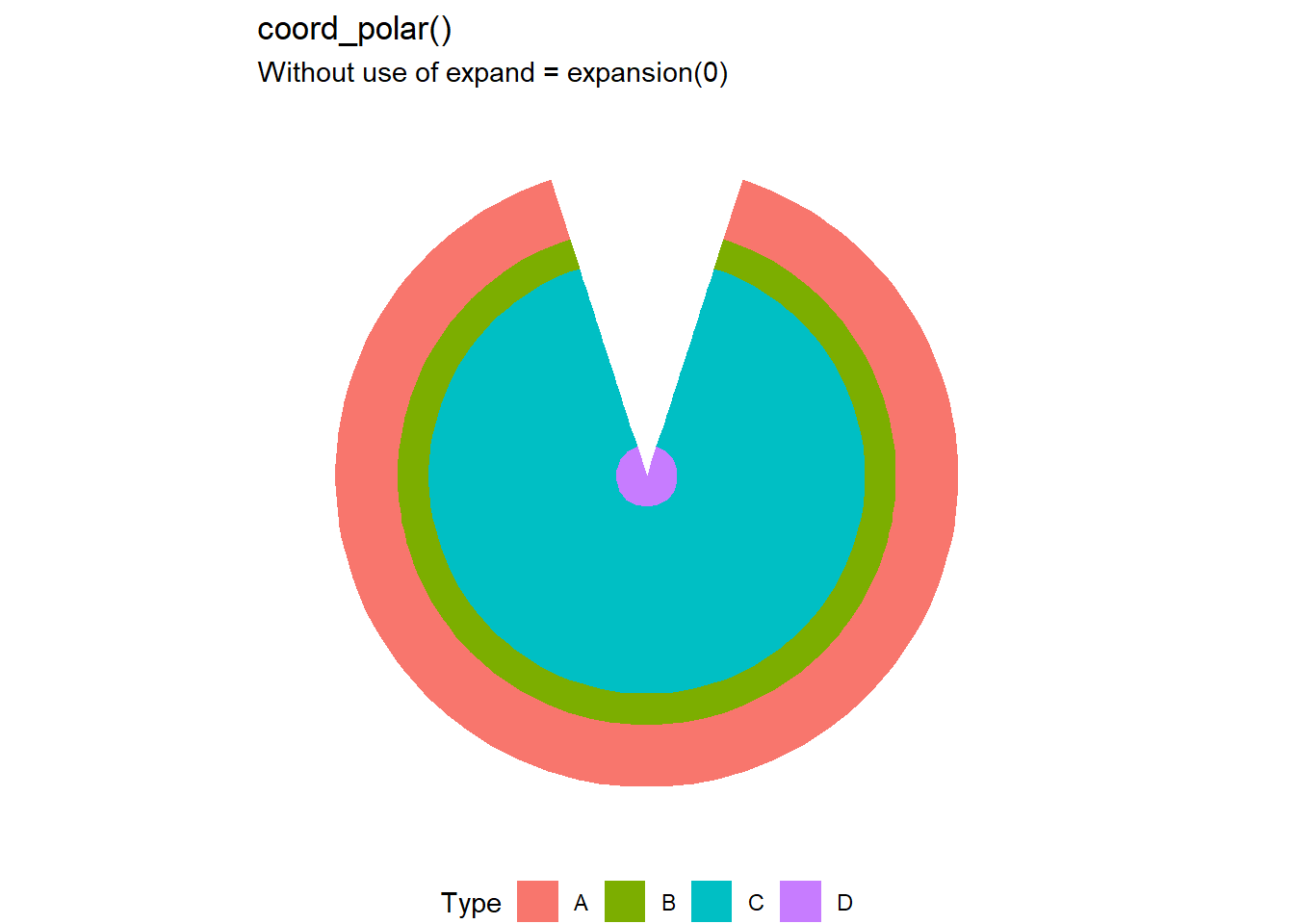
g2 + 
  coord_polar() +
  labs(title = "coord_polar()",
       subtitle = "Without use of expand = expansion(0)")

g2 + 
  coord_polar() +
  scale_x_discrete(expand = expansion(0)) +
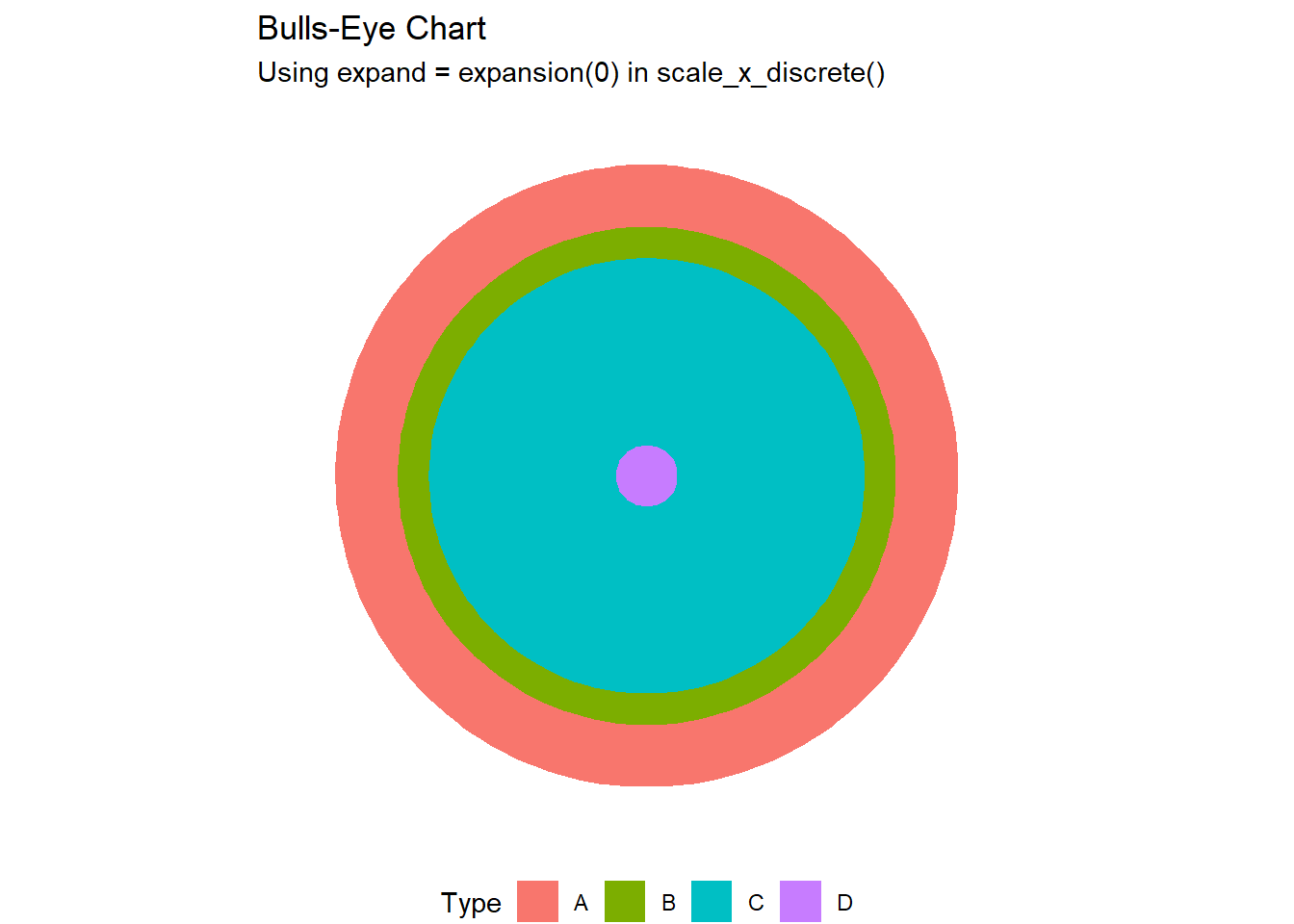
  labs(title = "Bulls-Eye Chart",
       subtitle = "Using expand = expansion(0) in scale_x_discrete()")

g2 + 
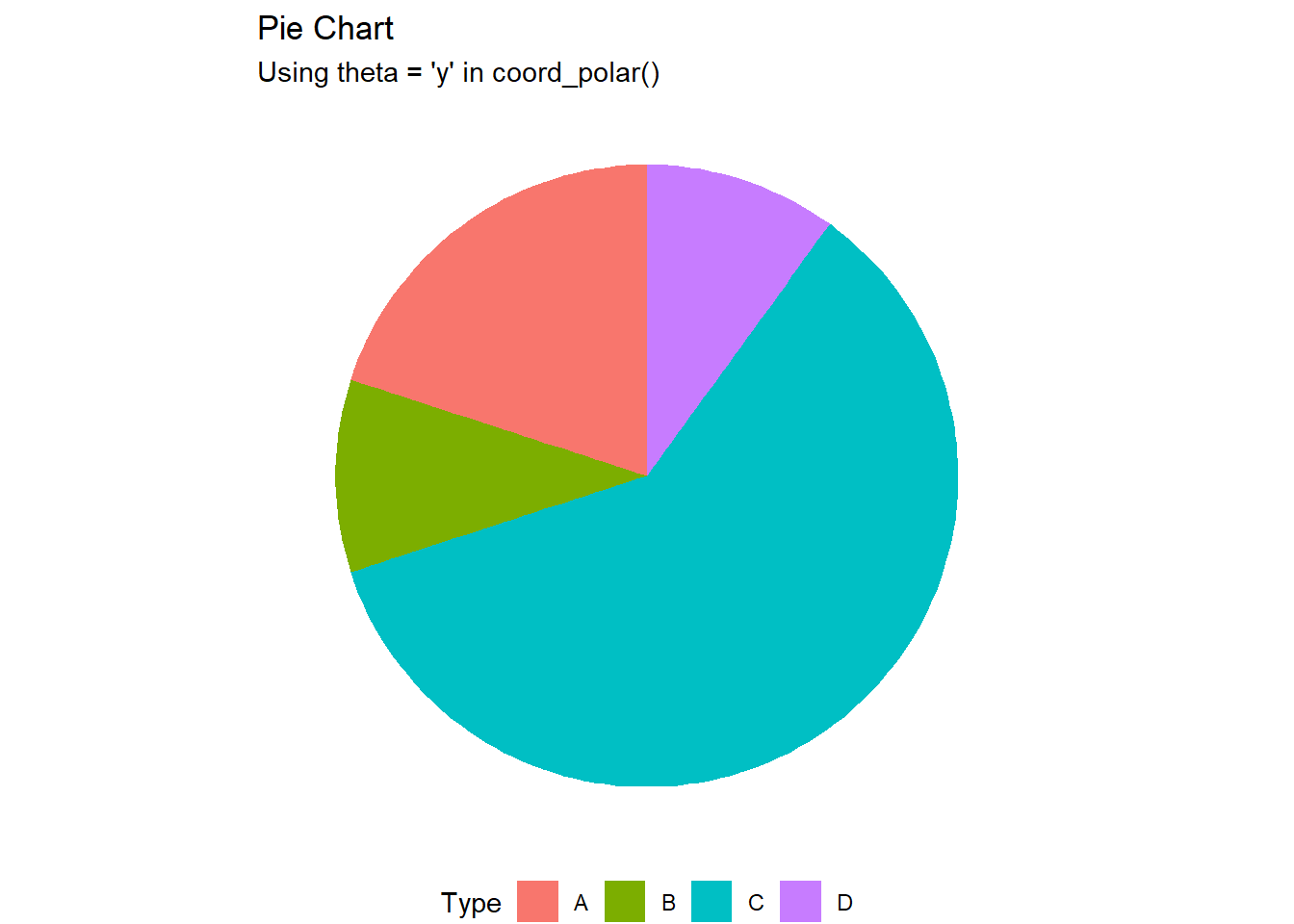
  coord_polar(theta = "y") +
  labs(title = "Pie Chart",
       subtitle = "Using theta = 'y' in coord_polar()")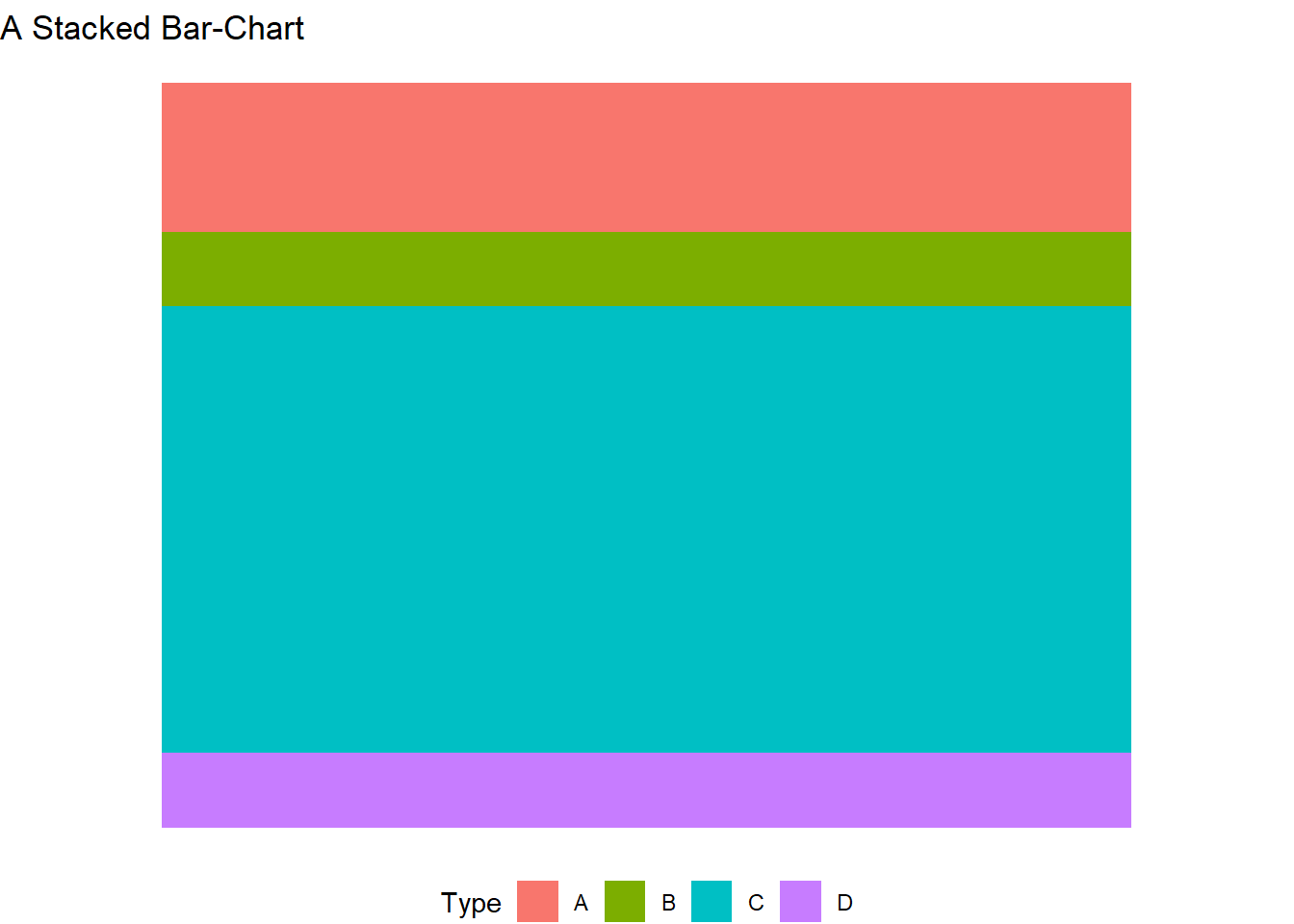
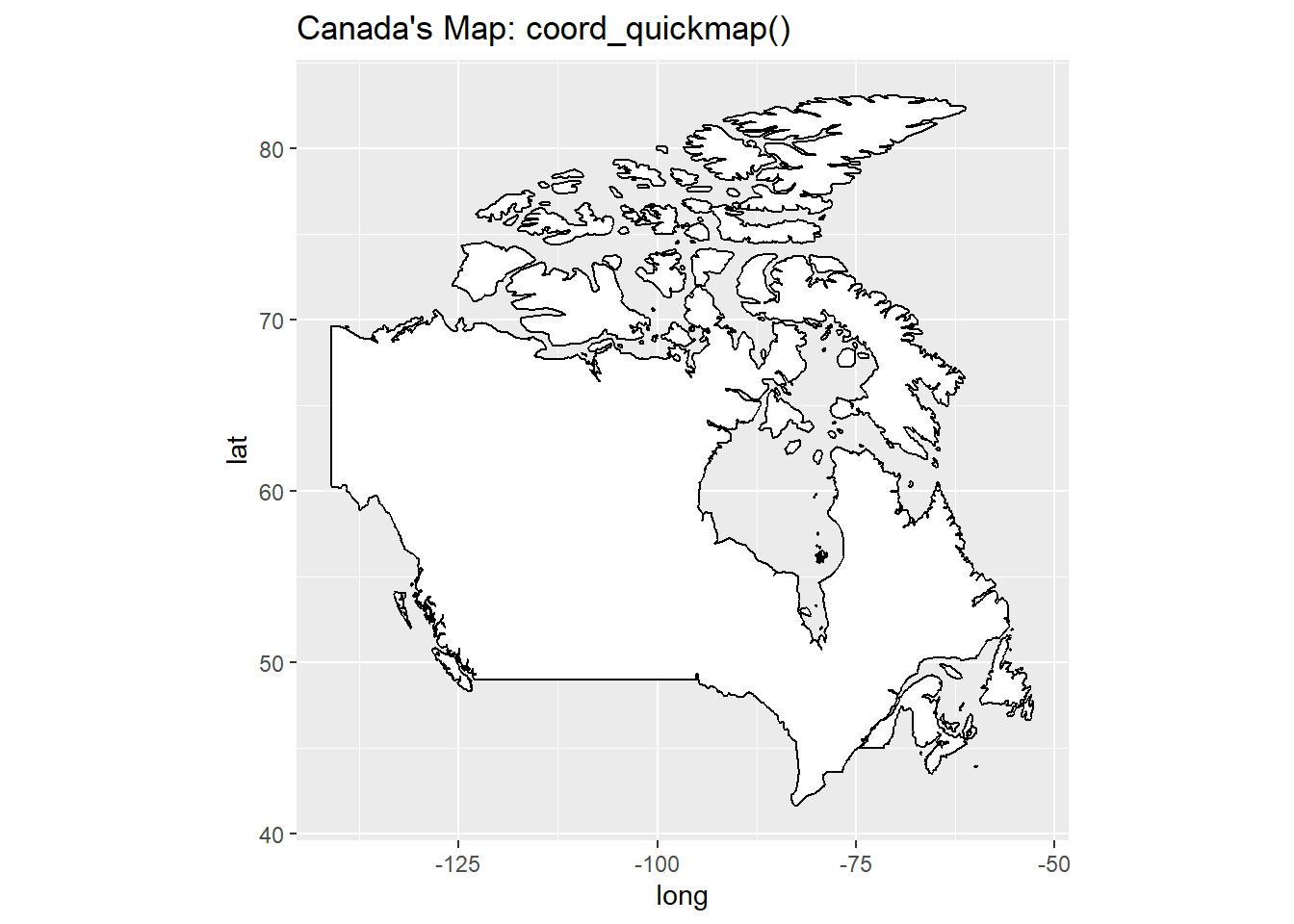
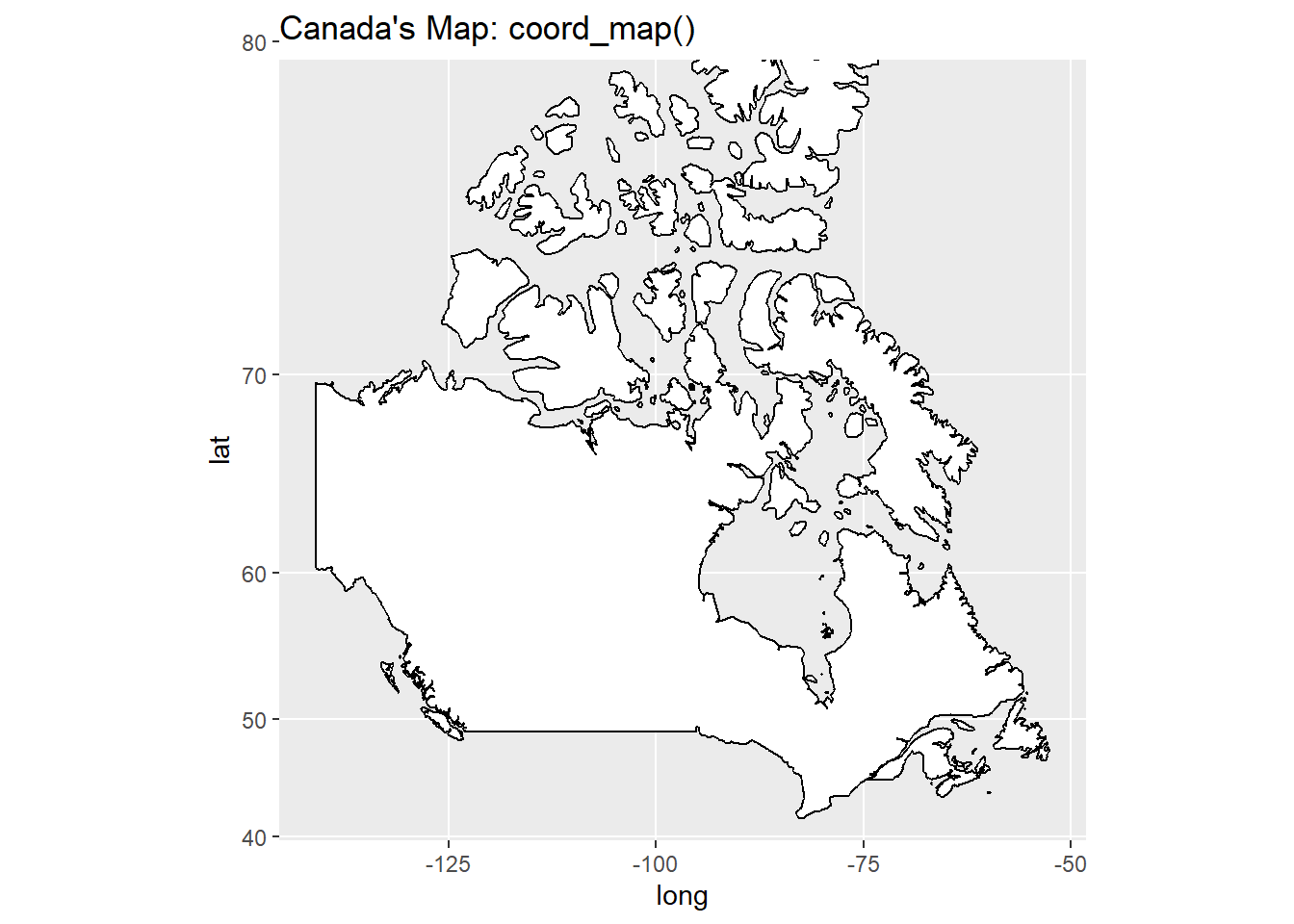
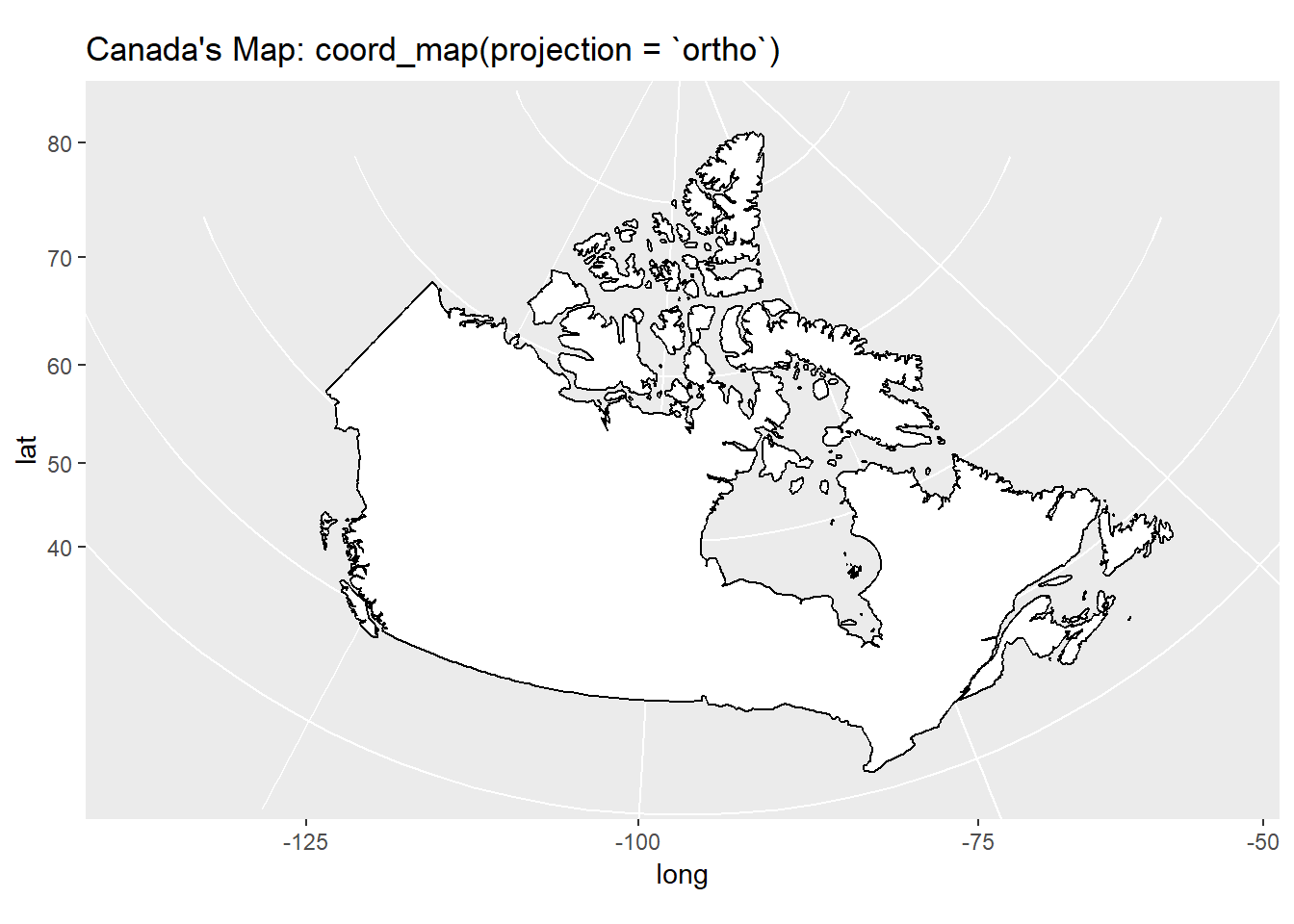
(a) A Stacked bar chart
(b) Chart with coord_polar()
(c) Bulls-Eye Chart
(d) Pie-Chart
Figure 8: Using polar coordinates

15.2.3 Map projections with coord_map()

Here, in Figure 9, we show the map of Canada with different projections.

Code
g3 <- map_data(
  database = "world",
  regions = "canada"
) |> 
  ggplot(
    aes(
      x = long,
      y = lat,
      group = group
    )
  ) +
  geom_polygon(
    fill = "white",
    colour = "black"
  ) +
  theme(legend.position = "none") +
  labs(title = "Canada's Map: coord_cartesian()")

g3 + 
  coord_quickmap() +
  labs(title = "Canada's Map: coord_quickmap()")

g3 + 
  coord_map() +
  labs(title = "Canada's Map: coord_map()")

g3 + 
  coord_map("ortho") +
  labs(title = "Canada's Map: coord_map(projection = `ortho`)")
(a) Base map in coord_cartesian()
(b) coord_quickmap()
(c) coord_map()
Figure 9: Map of Canada with different coordinates